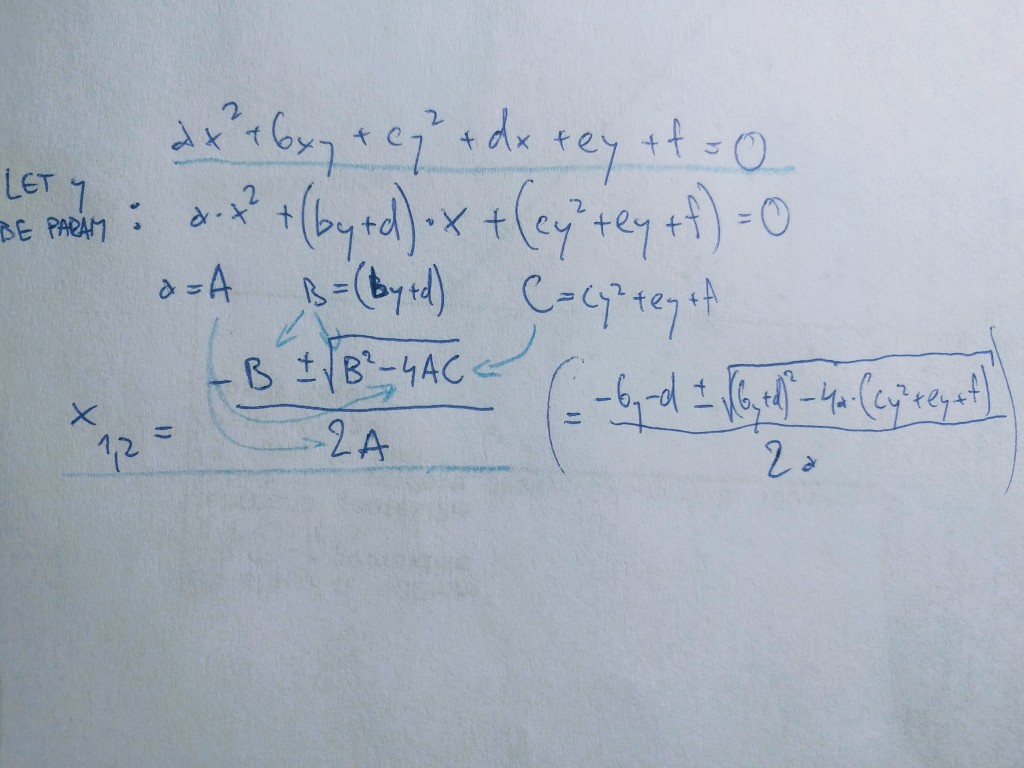Václav Železník: Creating an Ellipse given by 5 points
There is only one component that let’s you create an ellipse in Grasshopper. It requires both radiuses and its center. I think that is quite a difficult requirement if you are looking for some specific output, so I tried to explore other solutions. One of them is deforming a circle, that can create an ellipse, but that doesn’t ease the pain of center and radiuses.
WARNING: Lots of maths incoming
So, let’s start from the bottom:
General ellipse is defined by 5 points in a plane and its equation is:
Let’s use the points coordinates as X and Y. This gives us 5 LINEAR equations with 6 unknowns A, B, C, D, E, F.
Note that we are treating x^2, x*y, y^2, x and y as coeficients of the equations. We can imagine n. 1 in front of F.
Since all 5 points lie on the same ellipse, the linear equations must have common solution. From this, we see that the equation of the ellipse is given by setting the determinant of the matrix of coefficients of the 6 equations to 0. (More here)
HAH determinant – what is that? I don’t know (lookie here), all I know is how to calculate it:
In the case of a 2 × 2 matrix the determinant may be defined as
Let’s try it on a 3×3 matrix – I pick a and remove the column and row it is in and recieve a 2×2 matrix which is explained above. I hope this isn’t so difficult.
BUT our matrix is 6×6 AaAahH pAnIC.
So what! I use the above method on the 6×6 matrix. The blued determinants are 5×5 matrix each unique. Note the switching signs, I had a lot of trouble before I noticed these.
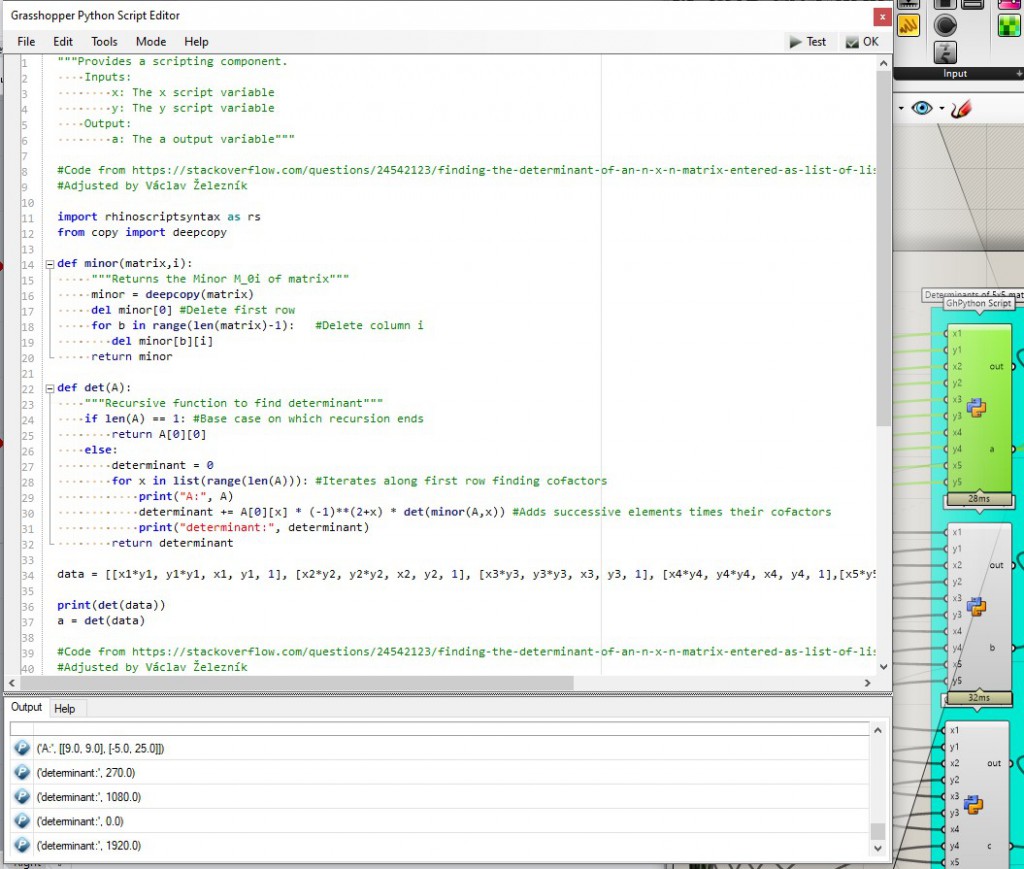
The 5×5 matrix determinats are fully composed of numbers, that’s perfect, because I can implement the algorythm in PythonScript.
As you can see, there is a lot of inputs – all the individual coordinates of the 5 points. These create the 1st 5×5 matrix (line 34; the blue one, you remember?). Then the recursive function det is called, it calls another function – minor. It decomposes the 5×5 matrix to 4×4, then 3×3, 2×2 by removing the rows and collumns every time and then returns the value of our desired determinant. Switch signes for det’s b, d and f (yes, that’s where the trouble came from).
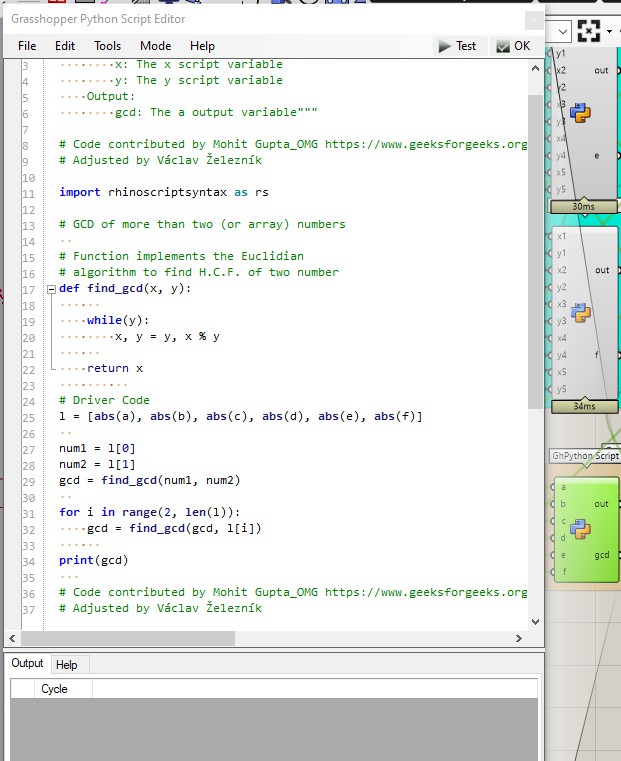
This is what happens in all of the 6 PythonScript boxes. Another script finds the Greatest Common Divisor of the determinants, just to have nicer and smaller numbers.
I am not entirely familiar with this code, but I couldn’t forget the absolute value because there may be some negative numbers, I do not want to divide with those (#staypositive). We done with Python here.
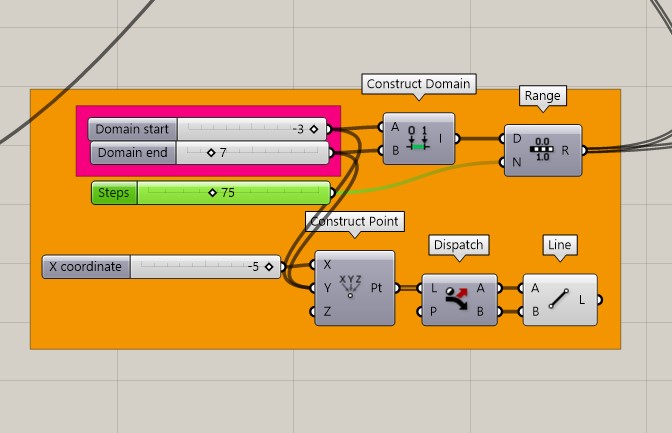
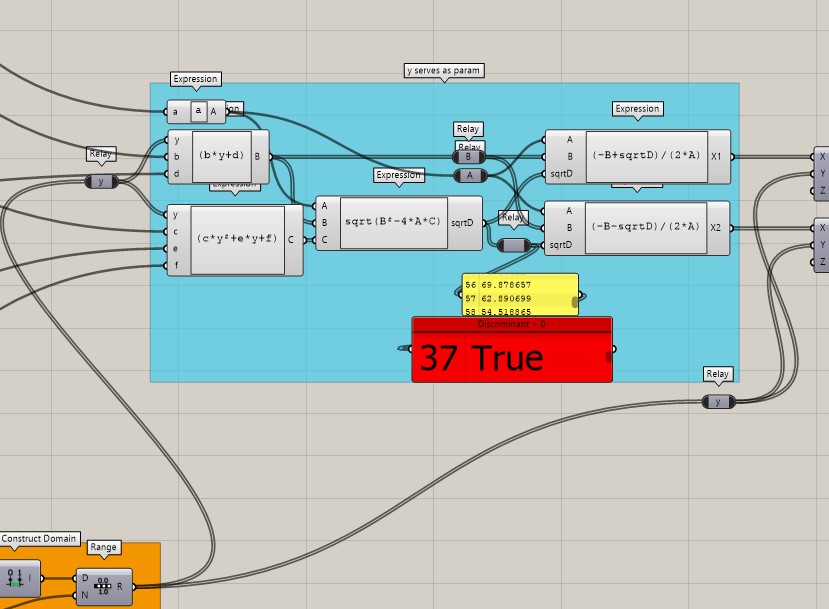
Up next is to make some points. More maths!
Here, I create some values for y coordinates and a Line for clarification where the values at.
Next, general equation and the well-known formula meet each other:
I express x and use y as a parameter. Note the condition that Discriminant has to be >=0. Feeding the expressions!
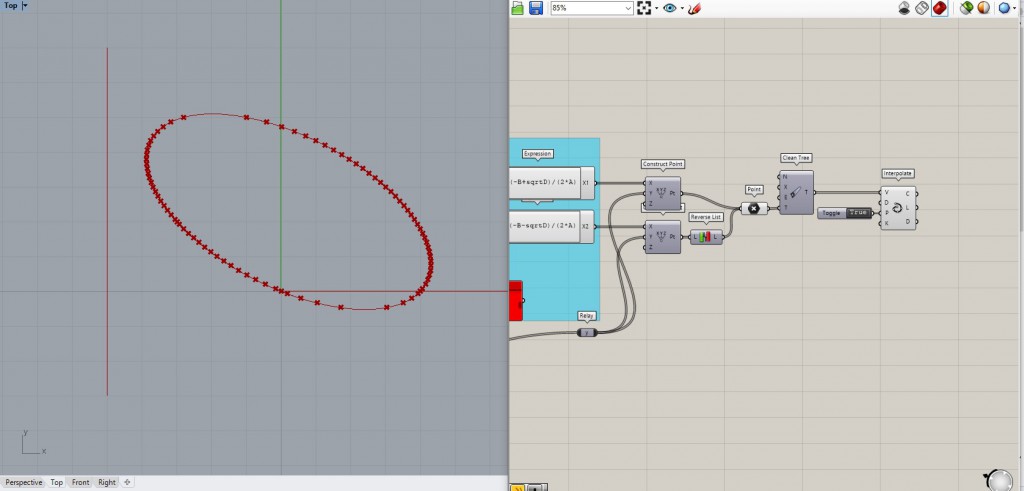
I create the points, Reverse one of the point lists get rid of the null items and Interpolate, periodically and here you are, ELLIPSE!
If you try switching some signs, some hyperbolas appear, too!
Try out the Galapagos script too, it will waste your time very well :D
Železník_CADIV_5PtEllipse_script
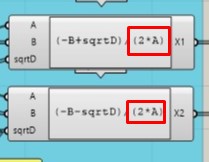
Fun fact: I spent like 4 hours trying to figure out what am I doing wrong – I forgot to add brackets here:

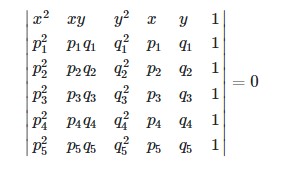

![{\displaystyle {\begin{aligned}|A|={\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}&=a\,{\begin{vmatrix}\Box &\Box &\Box \\\Box &e&f\\\Box &h&i\end{vmatrix}}-b\,{\begin{vmatrix}\Box &\Box &\Box \\d&\Box &f\\g&\Box &i\end{vmatrix}}+c\,{\begin{vmatrix}\Box &\Box &\Box \\d&e&\Box \\g&h&\Box \end{vmatrix}}\\[3pt]&=a\,{\begin{vmatrix}e&f\\h&i\end{vmatrix}}-b\,{\begin{vmatrix}d&f\\g&i\end{vmatrix}}+c\,{\begin{vmatrix}d&e\\g&h\end{vmatrix}}\\[3pt]&=aei+bfg+cdh-ceg-bdi-afh.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14f2f2a449d6d152ee71261e47551aa0a31c801e)