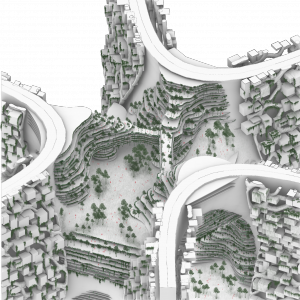
I wanted to remodel my studiowork (Fránek/Čančík studio) which was teamwork study of giant self sufficient skyscraper for 1 milion people. My part was to create structure in the middle of the skyscraper for civic amenities and public space. I have used archicad, and then rendering in Corona (not my work).
RHINO (arctic basic render) + Photoshop
———————————————————————————————————————
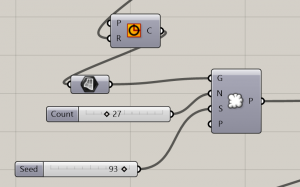
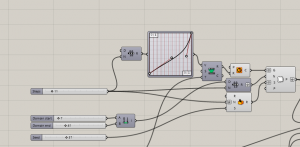
I have started with circle, then populate geometry for random points within the circle.
circle -> surface -> populate geometry
Then create metaballs above each point in the circle. Could be modify by genepool, seed etc.
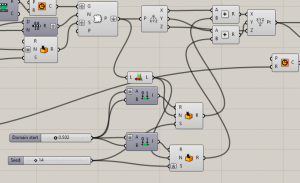
To create surface, we need to rebuild curve -> surface -> brep
The first part is done, we have organic structure with terraces that could be easily modified.
For the second part – there are two ways to achieve randomly placed greenery on the structure. For Modelling tutorial (my case) I will stay in grasshopper but I recomend to switch to Blender and do the whole greenery in render tutorial.
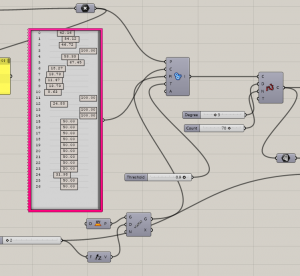
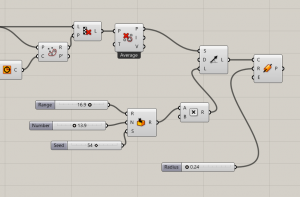
Grasshopper – I have started with the same circle, then remap numbers -> than create smaller circles inside -> modify by graph -> create points on the edges of the circles by populate geometry
Random points generator
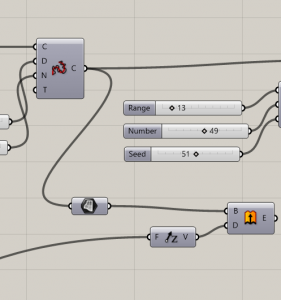
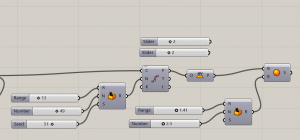
To achieve tree simulation I have put a cylinder over each point
And finally some spheres to simulate greenery on the buildings
Result:
Now lets try the better way -by scattering objects in blender
We need to activate scatter add-on so go to edit-> preferences -> add-ons -> Object: scatter object and enable the add-on
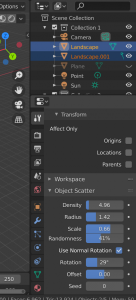
Then select object which we want to reproduce and then, select the surface/area etc. Press F3 on your keyboard and type scatter, now you can simply populate object on your surface/brep. You can modify density, size, randomness etc.
Example of random placed objects
There you can change the values
download file: CAD IV pecháček