Rainpipe Pavilion

1. The Idea

Once I visited the sea organ in Zadar and was really surprised of the atmosphere this installation evoked. In contrast to the hectic tourism in the city, here everyone quietly set on the ground and listend to the calming sounds of the sea and the organ.

Image II: Recording the Sea Organ (Morske Orgulje), Paresh, 2017

The problems I witnessed with this instrument were that the notes did not accord to a scale and sounded partly dissonant. Furthermore such an installation is only possible at the coastline of a sea and rather limited in its flexibility as it’s a solid structure that is hard to move.

Video I: GSM – Sea Organ (Morske Orgulje), Global Sound Movement, 2017

In conclusion I decided to make also a structure that interacts with natural element whilst being easily moveable and only playing wanted frequencies. As a result I came up with the Rainpipe Pavilion:

On top a dome shaped aluminium roof protects the visitor from rain. It lets light into the pavilion with a round window whilst transferring the impulses of raindrops via flaps down in the system.

The flaps are connected with a selected amount of aluminium pipes under the roof via plastic handles.

The pipes are the sound bodies of the pavillon and are activated by the rain. They are in bundles of 36 with increasing length. Every length produces a different frequency resulting in a note. By picking only certain notes (marked in purple) we can avoid dissonant sounds. This introduces a pattern that is repeatedly used in a spiral shape.

2. Challenges and Problems

The shape should be an adjustable spiral that has the same spacing in between the arms to create a walking path into the middle of the pavilion. It should host a number of pipes dividable by 12 (amount of half tones in a scale)
The frequencies of the wanted notes have to be calculated
The frequencies of each pipe have to be calculated for the parameters of material, thickness, radius and height according to the formula for pipe vibrations by Noor Fariza Saari, Azma Putra, Irianto, Reduan Mat Dan, Muhammad Agus Zeli, Roszaidi Ramlan, Nawal Aswan Abdul Jalil, Safarudin Herawan based on the Euler–Bernoulli beam theory
The note patterns should be easy to change with minimal inputs to accustom the pavilion to its current location and purpose
- f.i. at a sad occasion the pavillon should play minor scales
The pavilion has to have supporting poles which are going through the longest, non active pipes
- f.i. when a scale with the note C3 is being played the stands must go through C#3
The pipes need to be connected to each other for structural stability. The connections must be at the acoustic centres of each pipe to ensure maximum vibration
The dome roof should feature flaps that are directly above a group of two rays (radial alignment of four pipes)

3. Possible Solutions

1. To create the basic shape of the pavilion I created a spiral by moving a ray repeatedly in on direction using the component series. After that I rotated it 1080° using range. By dividing this rotation in a certain amount of steps I can determine the number of whole scales (including repetition of scales) in the structure

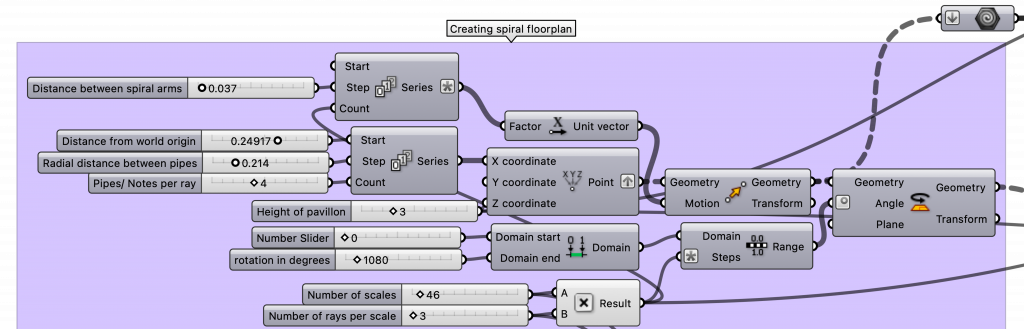
Video II: What if we do more rotations?

2. I selected at the beginning a note range from C3 to B5 (can be changed later depending on wanted pipe length) and applied the formula f = f0 * 2^(n/12) to get the frequencies of the notes and half notes in my range.

f = the searched frequency
f0 = a frequency of a reference note, f.i. C3
n = the half note steps away from that note
To do the conversion 36 times (total amount of notes) I used a series component

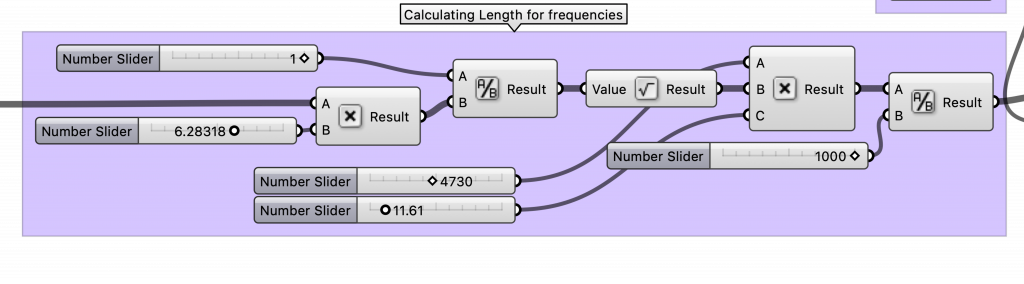
Image VII: Conversion of notes to frequencies

3. To convert the frequencies to lengths I used the formula for vibrating pipes: L= β * (1/(2*pi*f)^0.5 * ((EI)/ ρ*A)^1/4 which results in this formula if you put in all constants: L= 4730 * (1/(2*pi*f)^0.5 * 11,61

L = Length of pipes (m)
f = Frequency
β = Moden-constant ≈ 4.730 (for pipes)
E = Modulus of Elasticity for aluminium ≈ 6.9×1010 Pa6.9×1010Pa
ρ = Density of aluminium ≈ 2700 kg/m³
I = Moment of Inertia ≈ 4,7×10⁻⁶m⁴
A = Cross-Sectional Area ≈ 6.6×10⁻³m²
After the calculation of length the pipes are extruded by that factor

Image VIII: Calculating length for frequencies

4. First, to quickly change the notes played I introduced a piano like configuration of toggles which is combined into a pattern. Secondly the pipes are sorted into two groups using this pattern. Group A is transformed into active pipes that are connected to the roof. Group B remains normal pipes.

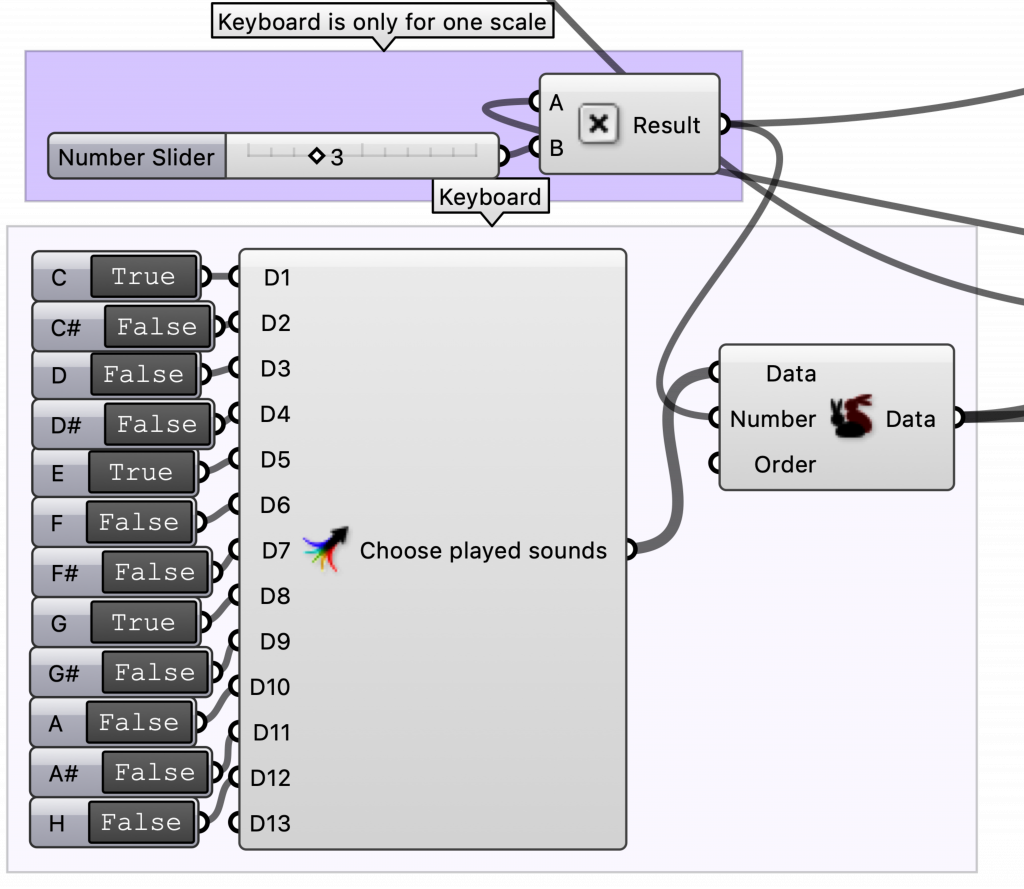
Using this we can vary the pattern and make the Rainpipe Pavilion play for instance different triads:

5. To know which pipes of the inactive ones are the longest I sorted them by size and divided that list in half at the index representing the number of all scales in the pavilion (look at step 1). After that I divided the pipes into points, projected them on the roof whilst moving their instances to the z-position zero. Connecting those results in supporting poles.

6. To create the structural system for holding the pipes we first need to find the two acoustic enters of each pipe. It is always approximately 25% from each end according to the beam theory. In conclusion I divided the pipes into four points, sorted out the second and the fourth one and connected them after applying a shift list component. As a result every pipe is connected to its neighbour’s acoustic center.

7. By selecting every first, fourth, fifth and eighth pipe in every two rays (in total eight pipes) I created the base for the flaps. This corners are projected on the roof and connected by lines.

4. Limits and Further Usage

The roof structure leaves right now many questions open. I still do not have answers as how the flaps work in reality and if the impact of raindrops will be enough. Also the pipe holding structure needs further development. But I am glad in the end that I had the possibility to make such a free and creative project. Besides the further development of this mechanical problems and limits the pavilion could also be paired with similar projects like the sea organ or maybe a wind chime pavilion?

5. Final rendering

Video III: Rainpipe Pavilion (reduced quality)

6. Sources

Image II: https://dev.globalsoundmovement.com/blog/1743-2/
Video I: https://www.youtube.com/watch?v=spImAJwSLC4&t=23s
Calculation of frequencies of pipes: https://www.sciencedirect.com/science/article/pii/S2405844024021790#:~:text=The%20natural%20frequency%20is%20given,of%20inertia%20given%20by%20Eq.
Calculation of note frequencies: https://techlib.com/reference/musical_note_frequencies.htm#:~:text=Starting%20at%20any%20note%20the,be%20positive%2C%20negative%20or%20zero.