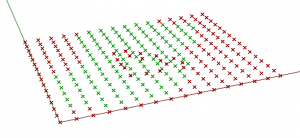
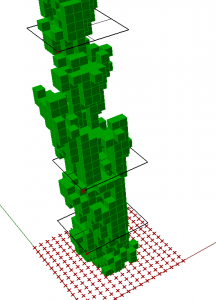
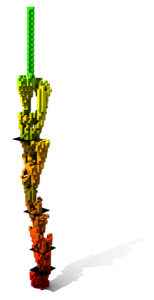Abstract tower simulator | CAD

OUR TARGET:

Our goal is to display a development of 2D cellular automata in 3D.

In this example is used a specific kind of CA – game of life. (but it can be easily changed in C# code)

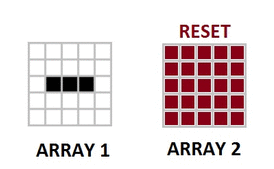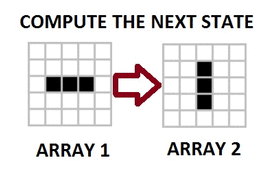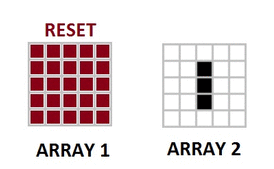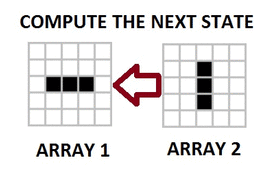
This Game of Life is an infinite two-dimensional orthogonal grid of square cells, each of which is in one of two possible states, alive or dead. Every cell interacts with its eight neighbours, which are the cells that are horizontally, vertically adjacent. At each step in time, the following transitions occur:

Any live cell with fewer than two live neighbours dies, as if caused by under-population.
Any live cell with two or three live neighbours lives on to the next generation.
Any live cell with more than three live neighbours dies, as if by overcrowding.
Any dead cell with exactly three live neighbours becomes a live cell, as if by reproduction.

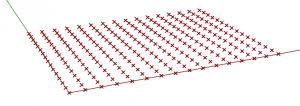
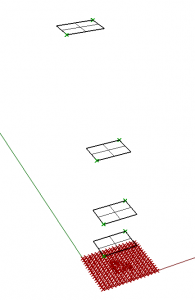
Points in Rhino determine initial state of CA.
Surfaces in Rhino are borders for CA.

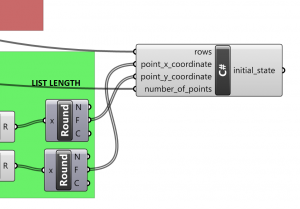
STEP 1

Create points in a grid position – ROWSxROWS (here 16×16 – from slider)

STEP 2

Set multiple points from Rhino.

Then get x and y coordinates of points.

Find out if a point is inside of the grid of points.

If the point is inside, we get its x and y coordinates.
If not we get null coordinates.

STEP 3

Find out in which cell lie point using C# code.

If point lie in cell we get number one (living cell).
If not, we get zero (dead cell).

Output of C# is list of living and dead cells. (initial state of game of life)

C# code:

int rows, List<int> point_x_coordinate, List<int> point_y_coordinate, int number_of_points, ref object initial_state

____________

//declaration of the array
int[] array = new int[rows * rows];

//transfer the point to the living cell
for (int j = 0; j < number_of_points; j++)
array[(point_y_coordinate[j] * rows) + point_x_coordinate[j]] = 1;

//elimination of incorrect output
array[0] = 0;

//output
initial_state = array;

STEP 4

Create two sliders.

Output of this is a data-tree list.
(for the sake of C#-code there is an addition of 2)

STEP 5

We will create bounds for cellular automata in this step. Cells outside of the bound die (in current state)

Set surface/s from Rhino.
Get two opposite vectors from this surface.
Output is a list of vectors (1 – lie in the surface, 0 doesn’t lie in the surface)

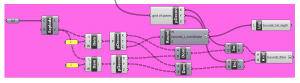
STEP 6

Join components from previous steps to the C# component.

STEP 7

In the next step we include a C# code.

C# code create two grids.
C# code record initial state of CA in the first grid.
The second grid look into the first grid and compute a new state of CA.
Then the first grid is cleared and filled by new state from the second grid.
etc…

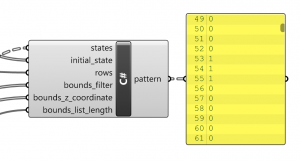
C# code:

int states, List<int> initial_state, int rows, List<int> bounds_filter, List<int> bounds_z_coordinate, int bounds_list_length, ref object pattern

____________

//declaration the size of arrays, to pretend of picking an element outside of the array
int size_array = (rows * rows – 1) + 2 * (rows);

//declaration of the array
int[] array = new int[size_array];

//declaration of the array2
int[] array2 = new int[size_array];

//definition of the initial state
for (int i = 0; i < (rows * rows – 1); i++)
array2[i] = initial_state[i];

//loading values to the array
for(int z = 0;z < states;z++){
//loading values to the array (in even states)
for(int i = (rows + 1);i < (size_array – rows – 1);i++){

//reset of the array from previous values
if(z > 0)array2[i] = 0;

//ensuring that edges of the array will be null
if((i % rows) == 0)array2[i] = 0;
else if(((i + 1) % (rows)) == 0)array2[i] = 0;
//conditons for dead cells
else if(array[i] == 0){
if((array[i – 1] + array[i + 1] + array[(i – rows) – 1] + array[(i – rows)] + array[(i – rows) + 1] + array[(i + rows) – 1] + array[(i + rows)] + array[(i + rows) + 1]) == 3
)array2[i] = 1;
}

//conditions for living cells
else if(array[i] == 1){
if(((array[i – 1] + array[i + 1] + array[(i – rows) – 1] + array[(i – rows)] + array[(i – rows) + 1] + array[(i + rows) – 1] + array[(i + rows)] + array[(i + rows) + 1]) == 3) ||
((array[i – 1] + array[i + 1] + array[(i – rows) – 1] + array[(i – rows)] + array[(i – rows) + 1] + array[(i + rows) – 1] + array[(i + rows)] + array[(i + rows) + 1]) == 2)
)array2[i] = 1;
}
//nullify cells outside of the bound
for(int g = 0; g < (bounds_list_length);g++)
if(bounds_z_coordinate[g] == z){
for(int h = 0; h < (rows * rows);h++){
if(bounds_filter[(h + (g * rows * rows))] == 0) array2[h] = 0;
}
}
}
//loading values to the array (in odd states)
z++;
for(int i = (rows + 1);i < (size_array – rows – 1) && (z < states);i++){

//reset of the array from previous values
array[i] = 0;

//ensuring that edges of the array will be null
if((i % rows) == 0)array[i] = 0;
else if(((i + 1) % rows ) == 0)array[i] = 0;

//conditons for dead cells
else if(array2[i] == 0){
if((array2[i – 1] + array2[i + 1] + array2[(i – rows) – 1] + array2[(i – rows)] + array2[(i – rows) + 1] + array2[(i + rows) – 1] + array2[(i + rows)] + array2[(i + rows) + 1]) == 3
)array[i] = 1;
}

//conditions for living cells
if(array2[i] == 1){
if(((array2[i – 1] + array2[i + 1] + array2[(i – rows) – 1] + array2[(i – rows)] + array2[(i – rows) + 1] + array2[(i + rows) – 1] + array2[(i + rows)] + array2[(i + rows) + 1]) == 3) ||
((array2[i – 1] + array2[i + 1] + array2[(i – rows) – 1] + array2[(i – rows)] + array2[(i – rows) + 1] + array2[(i + rows) – 1] + array2[(i + rows)] + array2[(i + rows) + 1]) == 2)
)array[i] = 1;
}
}
//nullify cells outside of the bound
for(int g = 0; g < (bounds_list_length);g++)
if(bounds_z_coordinate[g] == z){
for(int h = 0; h < (rows * rows);h++){
if(bounds_filter[(h + (g * rows * rows))] == 0) array[h] = 0;
}
}
}

//conditions for output (output takes data from the array and the array2 in rotation)
if((states % 2) == 0){
pattern = array2;
}
else{
pattern = array;
}

STEP 8