The goal is to create an other-wordly looking structured landscape by using a triplyperiodic minimal surface function. The intented use for a video game environment, where you can fly around in the structure. For this purpose, the object will be also exported to Unreal Engine 4.
First, you will need to download some plugins. Get Millipede created by Panagiotis Michalatos, Weaverbird by Giulio Piacentino, 4D Noise by Giulio@McNeel and LunchBox by Nathan Miller.
https://www.creativemutation.com/millipede
https://www.giuliopiacentino.com/get-wb/
https://www.food4rhino.com/en/app/4d-noise
https://www.food4rhino.com/en/app/lunchbox
Creating the “Landscape” Shape
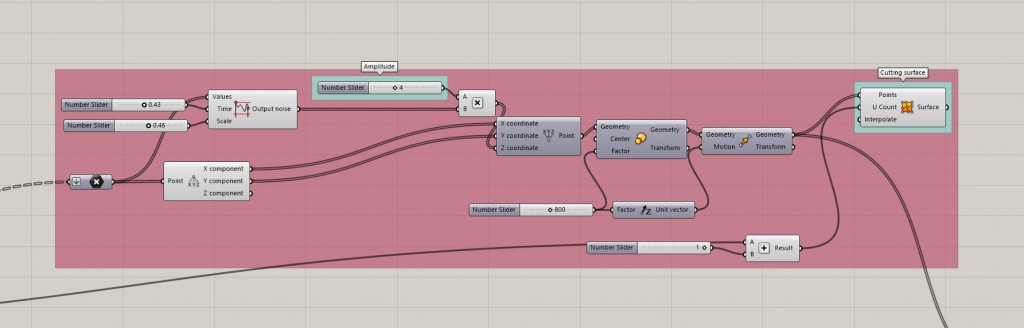
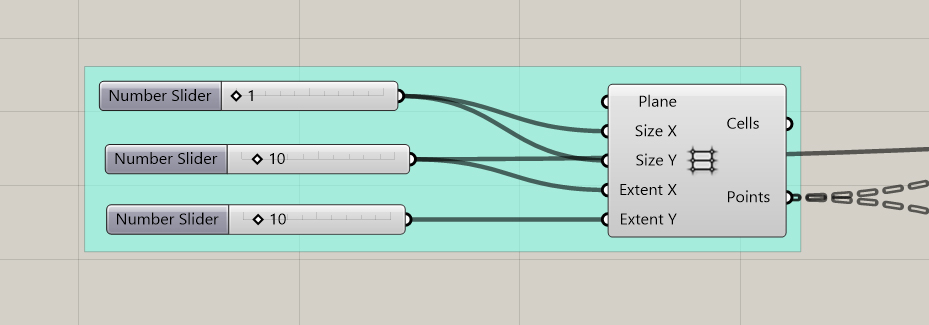
We will use a Rectangular Array of points, that will get offseted in the z direction using a Perlin Noise component from the 4D Noise plugin.
Create a Rectangular Array, define its dimensions, I used a 10×10 grid as bigger sizes were a bit slow to calculate in the end.
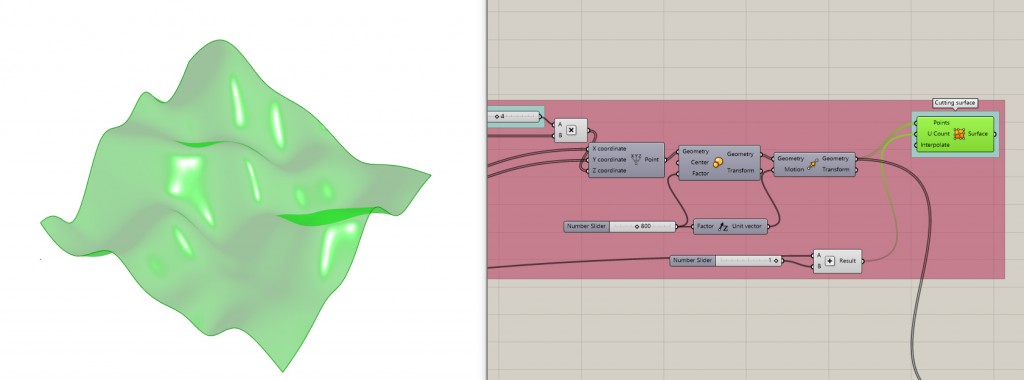
Flatten the data of the points and feed them to Perlin Noise, you can fiddle with the imput values later. Perlin Noise creates gradual random variation so it is ideal for landscape generation. The image below shows a way to deconstruct the point coordinates and construct it again with the noise changing the height (z value). It’s good to scale the geometry after using the Perlin Noise so you can easily see the changes made between 0-1 to the Perlin Noise. I then moved the points a bit upward, but that is just some playing around.
To better visualize this part of the process you can feed the points to Surface From Points component (the U count should then be the number of rows plus 1).
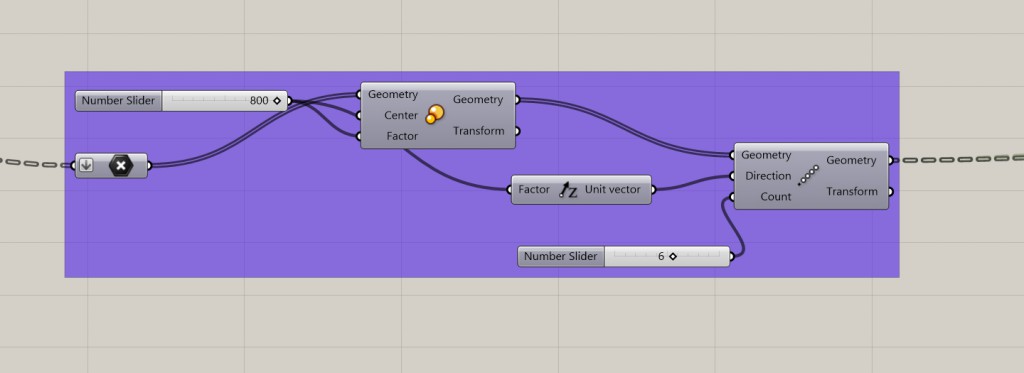
I wanted to create regularly placed boxes one on top of another placed “underneath” the landscape shape.
Take the original points from the Rectangular Array, scale them up and Linear Array them to the sky. I wanted the maximum height of 6 “stories” so that’s why the count is 6, but you can change it as you wish.
And so we get a box full of points, those will represent the placement of the boxes.
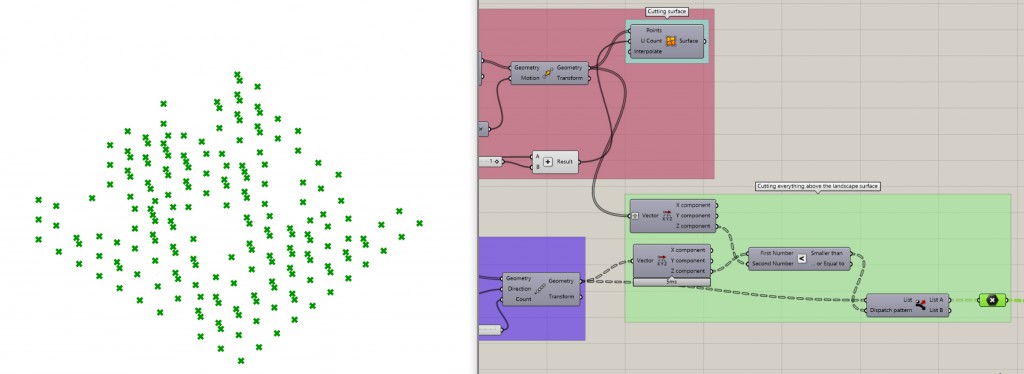
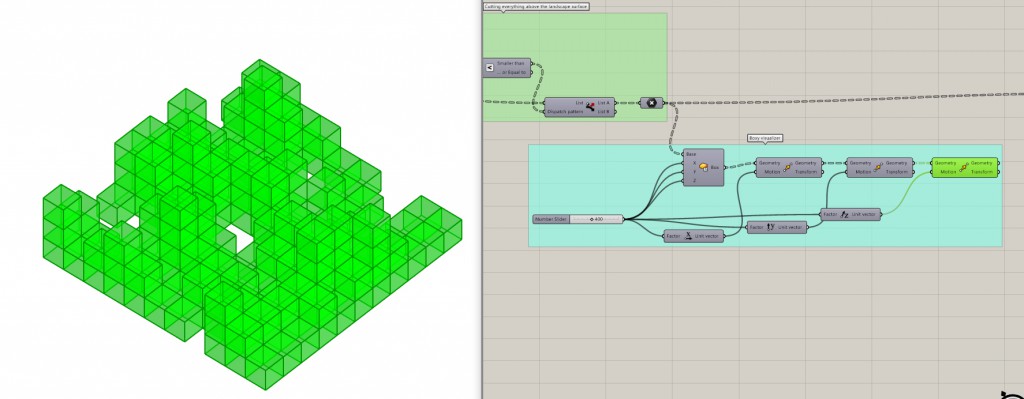
Now we will cull the points that are above the cutting surface points by comparing their z direction. It’s important to graft the data coming from the landscape points to get them on the same level of the data structure as the vertical linear arrays of points. Use Dispatch node to get rid of the unwanted points.
You can now visualize the “boxy” landscape by introducing a box node on each of the points. I only moved them around a bit so as to match to the final shape. This is a good preview of the result and it is still very fast.
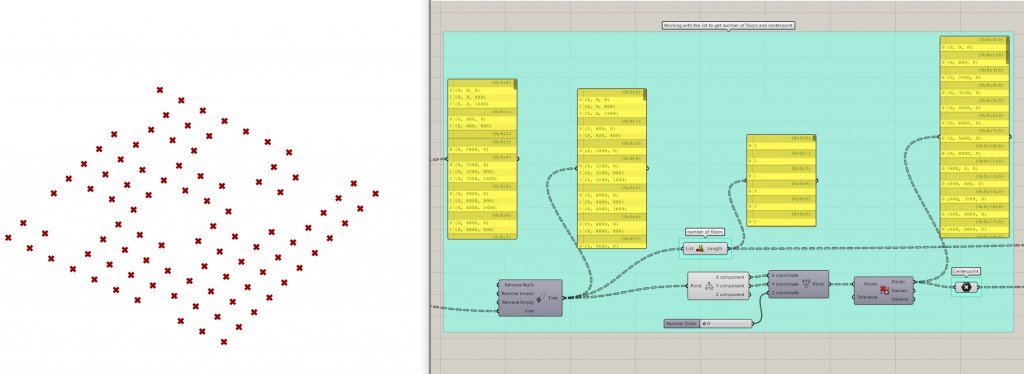
Next we need to work a bit on the lists of points we have. We need to get two output data: the number of floors stacked on every single point and the x and y location of this point (we will build from the ground up).
Use Clean Tree to remove empty lists (points that get culled by the landscape surface completely, these will remain empty). Next I wanted to only have one single point of the same x and y coordinates, so I forced them to the ground by changing their z coordinate to 0 and then used Cull Duplicates node.
Now we have the Center Point and The Number of Floors data, that fit together.
Creating a Triply Periodic Minimal Surface
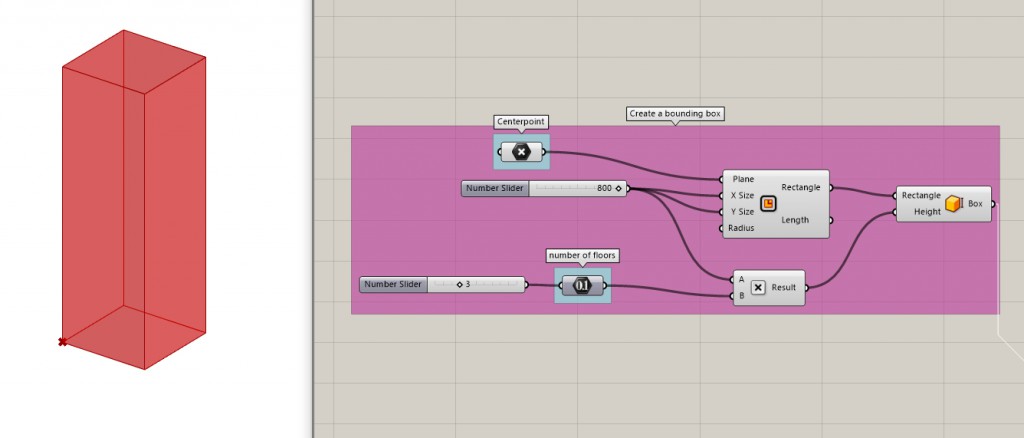
Start by creating a a box defined by a rectangle. The pivot point (Plane input) will be our Centerpoint and the height of the box will be the number of floors multiplied by the scale of one cell (I keep it at 800 the whole time).
It’s good to use one hardcoded point for the centerpoint and one number for the number of floors when you’re first working to get the tool ready, to reduce calculating time while working.
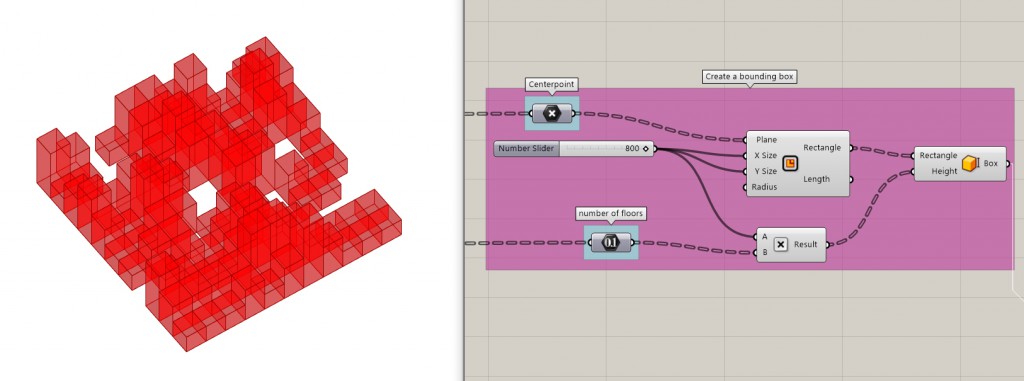
After plugging in the correct centerpoints and number of floors we get a geometry almost identical to what we have previewed in stacked boxes before (only these boxes are scaled up).
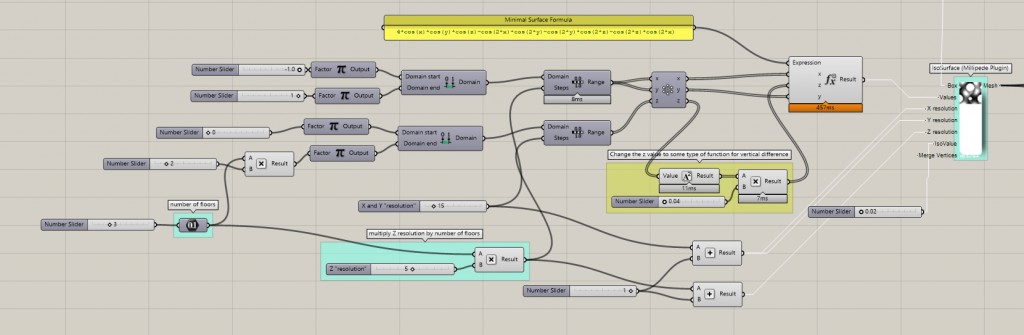
Now for the fun part. The core of everything is a mathematical formula for triply periodic minimal surface. There’s more of these bad guys around, you can read about them on the wikipedia or here https://wewanttolearn.wordpress.com/2016/03/17/triply-periodic-minimal-surfaces-_topology/ . It’s a fascinating subject but I won’t say anything more about them here. I gathered up some of these and wrote them to panels, so I can try them out one by one.

The heart of the operation is the Expression node. Plug in the formula you pick and set the x y and z parameters. This took me some hardbrain time, basically the goal was not to create a big shape and cut from it as that was a massive headache for my computer but to spit out a bunch of smaller towers already in the final shape of the landscape. To do this I plugged in the number of floors to the period when the formula is calculated.
Then plug the calculated result to the Isosurface node from the Millipede plugin, the bounding box comes in hand now.
You can work out the math from this image. If you want to increase the level of detail you can also fiddle with the X Y and Z resolution of the Isosurface.
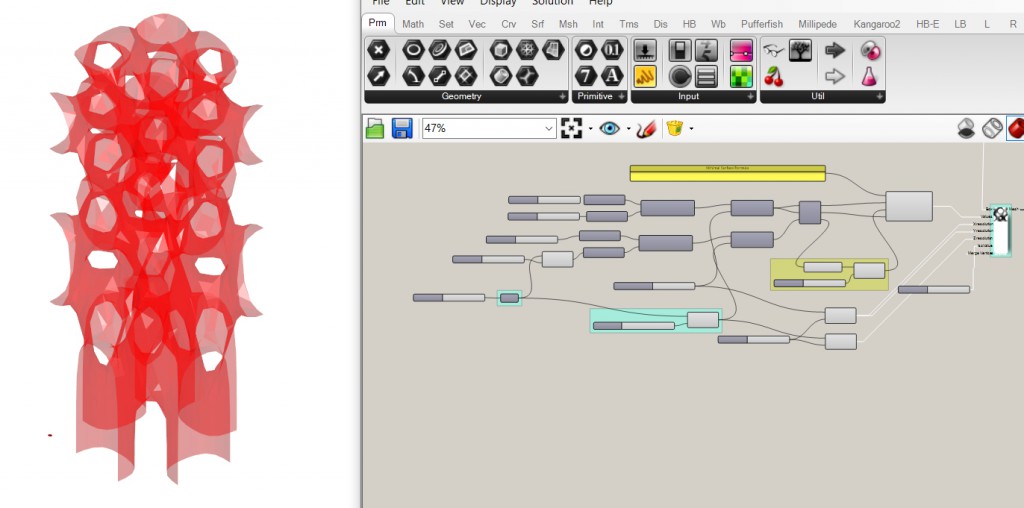
Sit back and watch grasshopper do its magic. Cool shapes coming in. I wanted a change in the vertical direction so I fiddled with the z coordinate by squaring it and multiplying it by some parameter, you can try out whatever you think of, but it should be a function of z to do something.
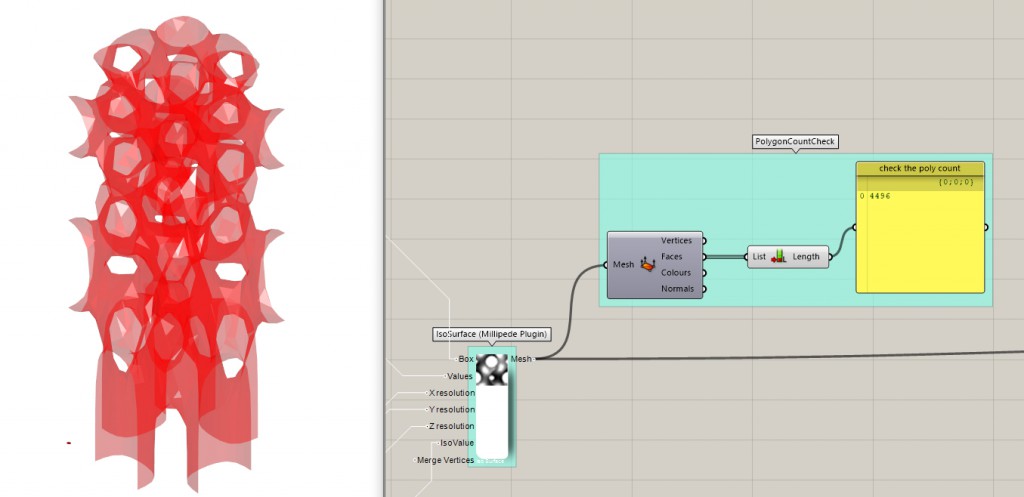
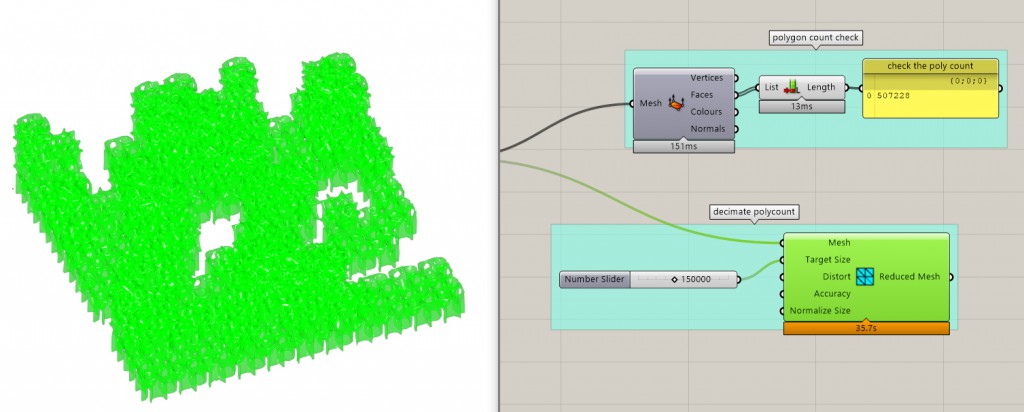
Good practice in game design, well a necessary practice actually, is keeping the polygon count of the mesh at minimum. You can use the Deconstruct Mesh node and check the List Length of the faces output to check the poly count. What is too much and what is not, I can’t really tell you, it always depends on the kind of game you’re working on and the hardware you’re optimalizing for. Keep at the minimum as much as you can basically.
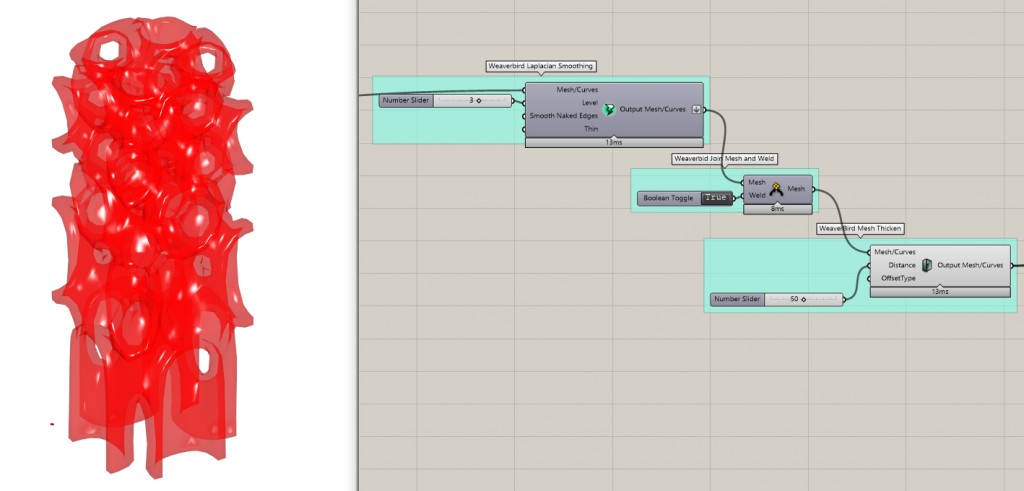
To smooth out the shape i use Laplacian Smoothing from the Weaverbird Plugin as it doesn’t increase the polygon count. Then Join Mesh and Weld all the “towers” together and Mesh Thicken the geometry to create a solid shape.
Check the polygon count now. Try not to cry. If it really hurts, you can try Mesh Reduce to some target size of polygons. Try not to cry about how much worse everything will look thou.
And voilà! It’s a triply periodic minimal surface landscape if I’ve ever seen one! (I actually haven’t, and it’s so… beautiful).
You can also plug in those other mathematical formula bad boys and see what happens. Something if you fiddle with some of the parameters it gets interesting.
A city of amphoras? Must have been the old greeks…

Thank you for your attention and have fun with your creations.
If you want to import the landscape into Unreal Engine, the simplest way is to export the object as an .obj file and then import it to UE4.
gh file: TriplyPeriodicMinimalSurfaceLandscape