Click to open a gif
Files – Grasshoppoer file: Sluneční-soustavafinal Rhino file: Untitled2,
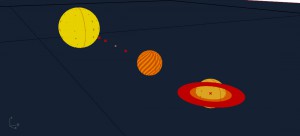
Můj projekt se opírá o obecnou teorii relativity, která říká, že gravitace je zakřivení časoprostoru. Takto se dají například vysvětlit odchylky ve tvarech trajektorií planet Sluneční soustavy. Myšlenka, že gravitace se projevuje vlastně geometricky, mě přivedla k nápadu ji zpracovat pomocí pluginu Rhina – Grasshopper. Projekt obahuje modely osmi planet soustavy + Slunce v jejím středu. Plocha umístěná pod úrovní planet znázorňuje časoprostor, který se zakřivuje podle aktuální polohy planet.
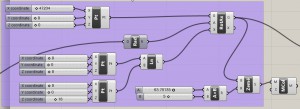
1) Pomocí komponentu (dále jen kp.) Rotate axis jsem vytvořil rotující bod kolem svislé přímky tvořené dvěma body. Na tento bod jsem “připnul” kouli představující planetu. Rotující bod má souřadnici-x rovnu poloměru elipsy, po které planeta obíhá.
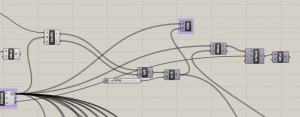
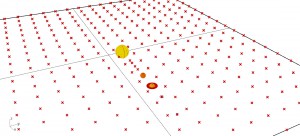
2) Pomocí kp. Vector2Pt jsem vytvořil vektory skládající se z bodů A a B. Bod A je středem aktuální planety, body B jsou body plochy časoprostoru (dále jen “plochy”). Tyto vektory jsou zobrazeny na obrázku. Plocha je tvořena urcitým počtem bodu. Dá se zvýšit její hustota.
3) Plochu jsem posunul níže pod planety. Jak je vidět z profilu, vektory zakřivují plochu v závislosti na poloze planet. Na obrázku jsou seřazena všechna vesmírná tělesa včetně Slunce na jedné přímce, takže vzniká největší zakřivení (největší “průhyb”)
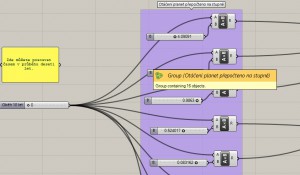
4) Planety se pohybují po svých drahách různými rychlostmi. V modelu se dá pohybovat soustavou v rámci deseti let. Kupříkladu Uran se za deset let dostane jen lehce přes osminu své cesty kolem Slunce. Naproti tomu Merkur za stejný čas stačí oběhnout kolem Slunce jedenačtyřicetkrát.
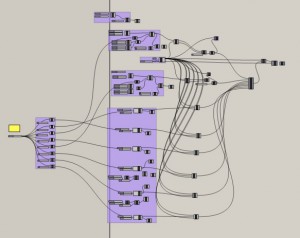
5) Parametrický pohled na síť bodu plochy.
VELIKOST PLANET JE SKUTEČNÁ VELIKOST VYNÁSOBENÁ OSMI. VZDÁLENOST OD SLUNCE JE KVŮLI PŘEHLEDNOSTI MODELU POUZE ORIENTAČNÍ.
Jiří Kulhavý / LS 2015 / vyučující: Bc. Šimon Prokop