Visualization of musical harmony

New update:

I´ve come across this musical theory from David Wallimann, check it out!
https://www.youtube.com/watch?v=G11t5nmNkMs

I think it really clicks with my own piece of theory regarding functional harmony.

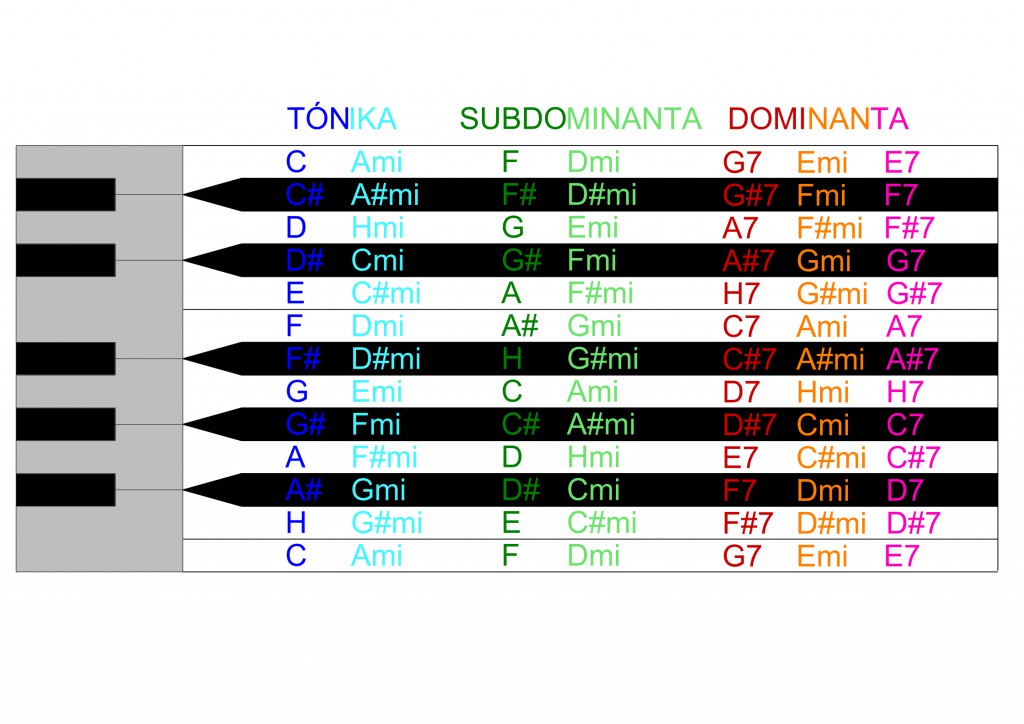
Tonic, the centric, calming, assuring, safe is blue. If you use the minor chord it gets light blue.
Subdominant is always a vector pointing somewhere, it´s growth, but subtle, it´s evolution.
Dominant is aggressive, demanding (the tonic of course), spiky (when flavoured), it´s the revolution.

There´s a little more on this topic here:

http://www.studioflorian.com/projekty/255-simon-prokop-guitar

and here:

http://www.studioflorian.com/projekty/305-simon-prokop-diagramusic

Download

Download:Chord_analysis_Tone_analysis_draft                Sound_blob

Abstract

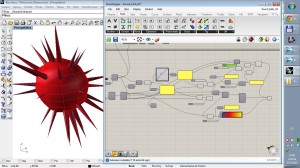
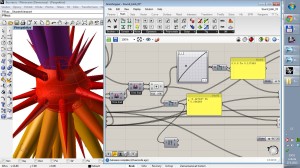
The aim of this project is to visualise the rules of classical functional musical harmony so that a player can precieve the rules behind the succesions of chords he or she playes. We are used to assign emotions to music we hear, however we can aslo assign them to visual impulses, forms and textures. The script should create a fluid animation of a ball-like body with a texture of spikes which corresponds to the musical function being played. The project is still ongoing so now there is a file with chord recognition and a draft of assingning them to their musical keys along with a sketch of the sound-blob now reacting to volume not harmony.

The Idea

I want to display variations of visually expressive structures in their relation to musical harmony and its rules. In another words I enforce virtual mass to behave in the way an observer could easily connect with music that gave birth to the mass. It is an education tool or just a visualiser for live playing.

Lately I experimented with live sound imput from FireFly plugin… Just a more accurate draft of where this project is heading to:

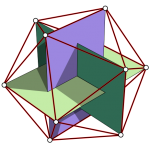
The Mass

I started with a sphere because of its naturaly coherent, central, basic, calm meaning which corresponds to musical qualities of tonic chord. Then I needed to add some expressive meaning to the mass so I started to work with Fuller’s sphere ( geodesic dome) simplified to an icosahedron because it still resembles a sphere but has edges and is easily extrudabe. The best way to create one is simply connect the points which are corners of 3 perpendicular golden rectangles.

The following Cartesian coordinates define the vertices of an icosahedron with edge-length 2, centered at the origin:

(0, ±1, ±φ)

(±1, ±φ, 0)

(±φ, 0, ±1)

where φ = (1 + √5) / 2 is the golden ratio.

The Steps

Then I used fractal triangulation to create so called “spikes”. Each face of the Fuller’s icosahedron got triangulated by a simple script using centerpoints. Resulting faces are again triangles so the proces can be repeated fractally. This feature garants many different outcomes and the complexity rises with each fractal step exponentialy which is useful since music usually escalates very quickly.

The Music

Aside of the visual problematics of this task there was a lot of work with “teaching” Grasshopper to recgnise different chords and their classification into keys. Since there is a finite number of keys for chords to be a part of and also some portions of chords belong to more than one key I decided to make a huge data tree with braches corresponding to each of the keys. Then, after characterising and recognising the chord Grasshopper can match its individual notes to the right branch/key. After that even a computer can recognise what musical function (tonic, subdominant or dominant) “is on” and manipulate the structure into a shape suitable to express the feeling of the current chord progression.

The last problem is to make it all work together. I need to get a MIDI signal from an instrument, feed it to the recognition script in Grasshopper and still spare some processor power to create the mass acording to the signal all in real time.