Concept and purpose of the project:
→ Work as a basis for a diploma thesis
→ Creation of a kindergarten in Český Brod
Shape concept:
→ Voronoi-shaped rooms with an enclosed atrium for a children’s yard
TARGET:
→ Creation of material variants of the Kindergarten solution according to the criteria of insolation and shape using the Galapagos component
____________________________________________________________________________________________________________
1. Creation of the shape:
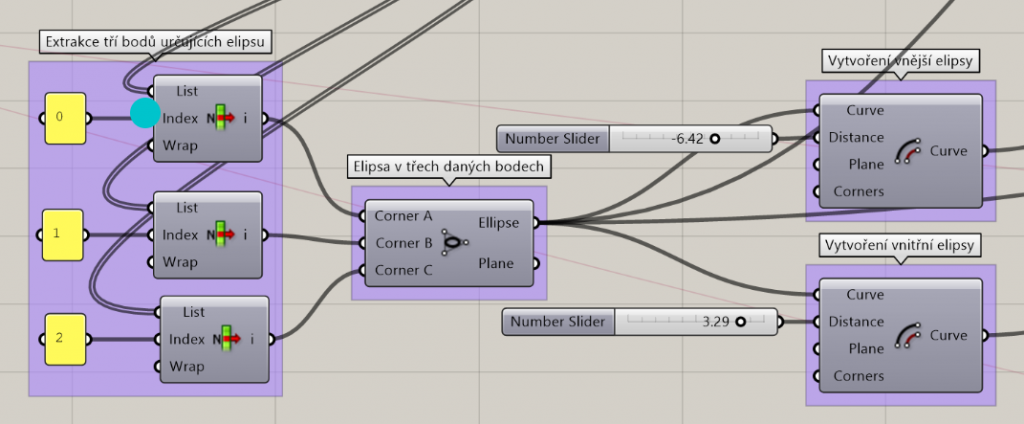
1a) Using the gene pool, I generate a trio of points that will create the main ellipse on which the individual rooms will be placed.
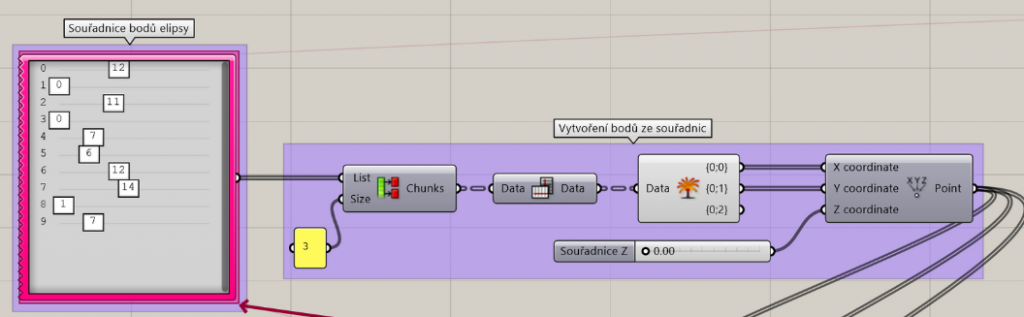
1b) Since I need to bound the cells to my voronoi shape, I create two more ellipses, one inside and one outside the original one.
1c) I divide all three ellipses into the same number of points = number of rooms.
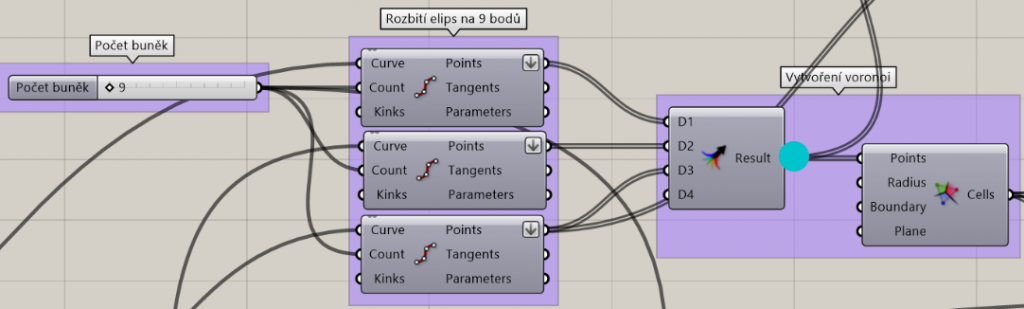
1d) I merge the points from the ellipses and create a Voronoi network from them.
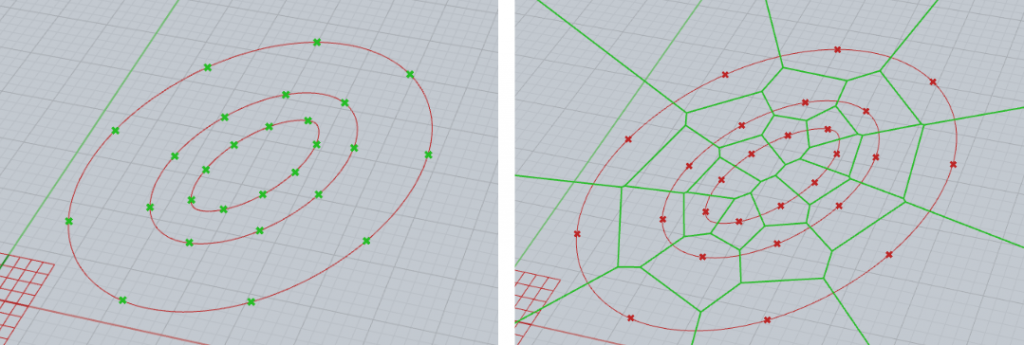
1e) I use the index to select the first 9 points, which are the points on the target ellipse that will form the mass.

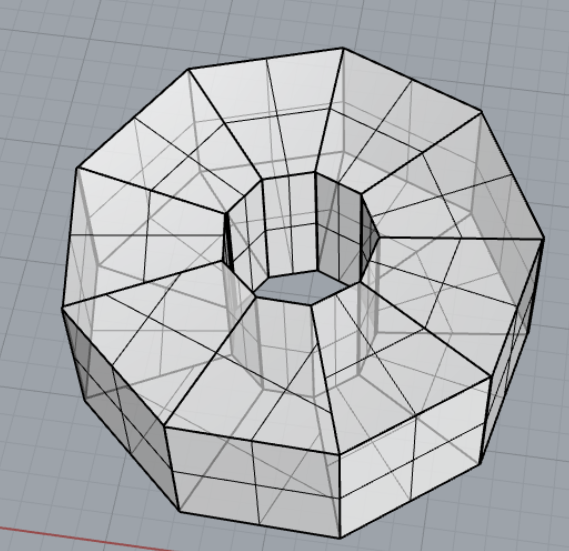
1f) Subsequently, I divide the separated cells at their vertices and create a surface from the resulting edges.
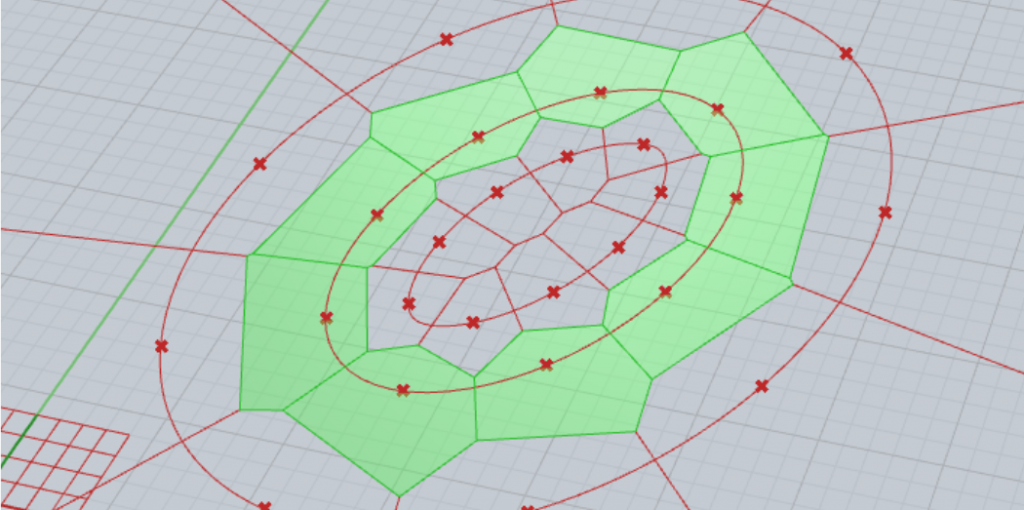
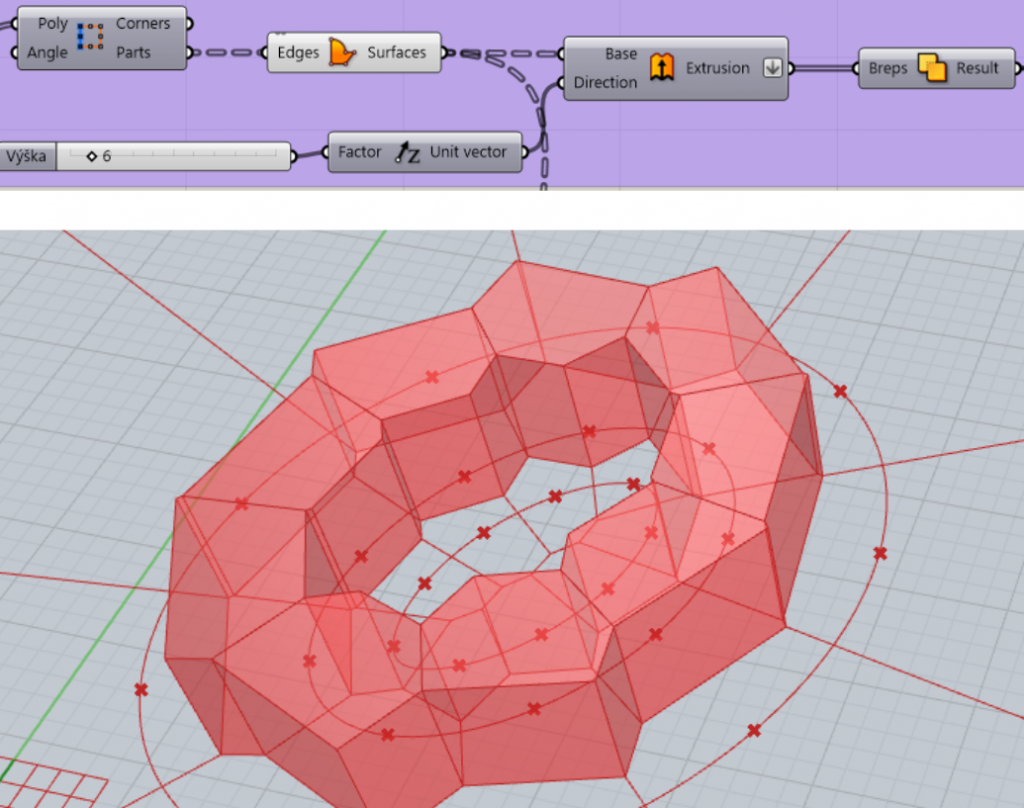
1g) Using the extrude component, I will pull out the floor plan shape to a height of 6m.
1h) I calculate the total surface area of the resulting shape.
____________________________________________________________________________________________________________
TEST #1
Using galapagos, I created a shape where I connected the gene pool to the input, which generates the coordinates of the points of the ellipse, and I set area maximization as fitness.
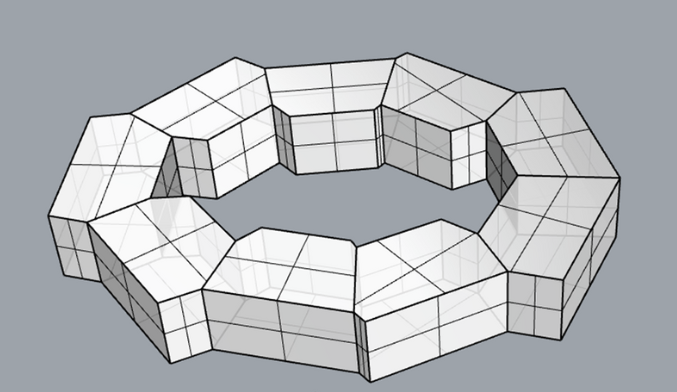
Result:
Maximum achievable surface area: 1625 m2
Knowledge:
A relatively symmetrical shape is created
All the cells are always slightly extended/retracted from each other
The shape corresponds to the original idea
Questions:
Is this the shape that corresponds to the best insolation?
____________________________________________________________________________________________________________
2. Solar verification with ladybug
2a) The first step is to get a weather link and the position of the sun near the target plot. I chose a point in the northwest of Prague because it was the closest available.
2b) To create the analysis, it was necessary to determine the period for which I want to maximize the impact of sunlight on the building. I chose December 21 as the date with the shortest day.
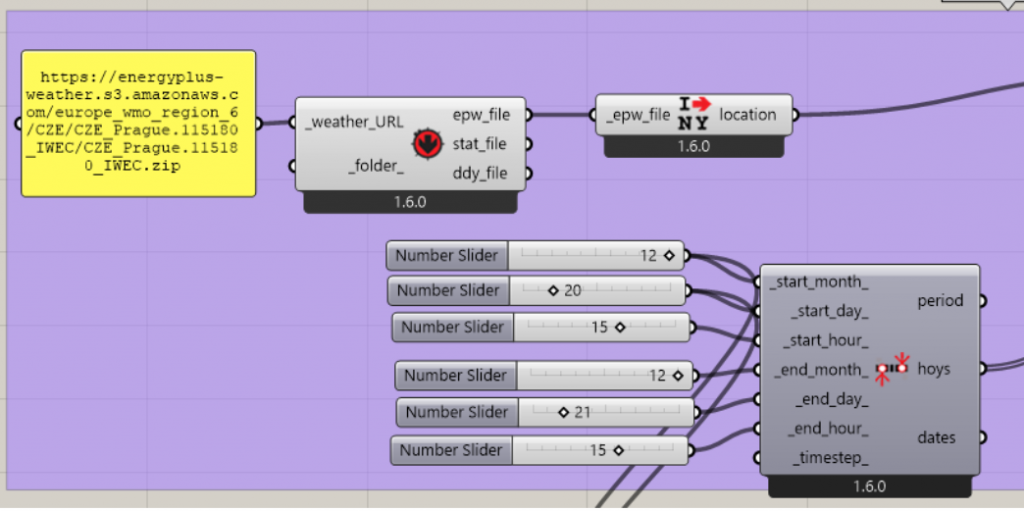
2c) To plot the path of the sun in this particular time period, I used a component designed for that.
2d) I did the analysis display on my model on a 1.6 meter grid. I started the program and could see the results.
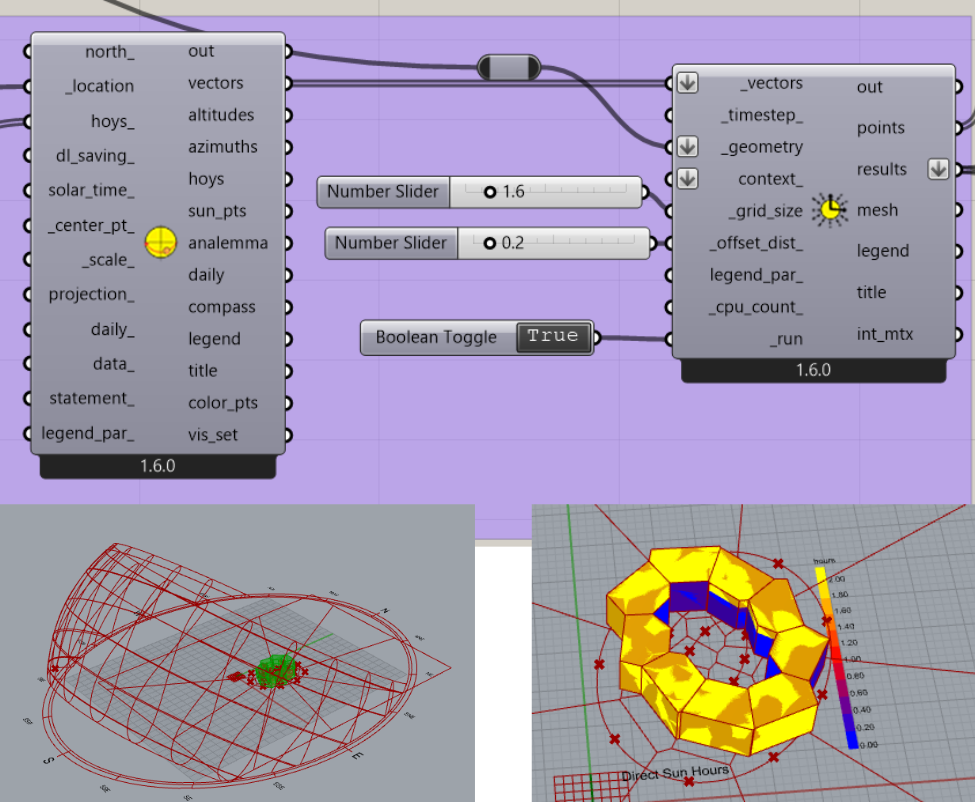
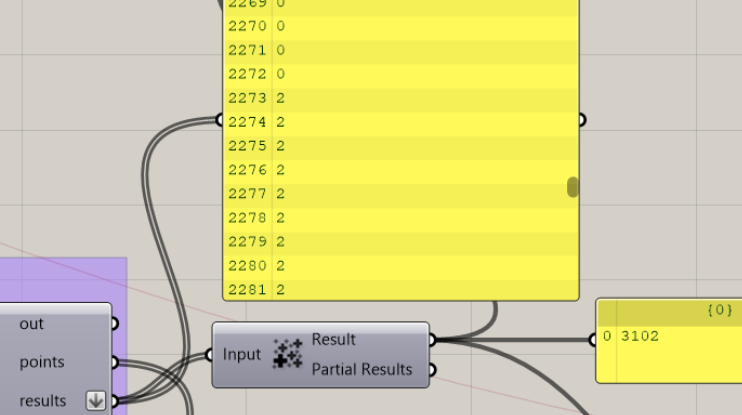
2e) For each shape, this component generates a number of points for which it evaluates the number of hours direct light falls on these points. (from 0 a.m. to 2 a.m.). I added these values to find out the total number of hours when the sun directly hits the facade.

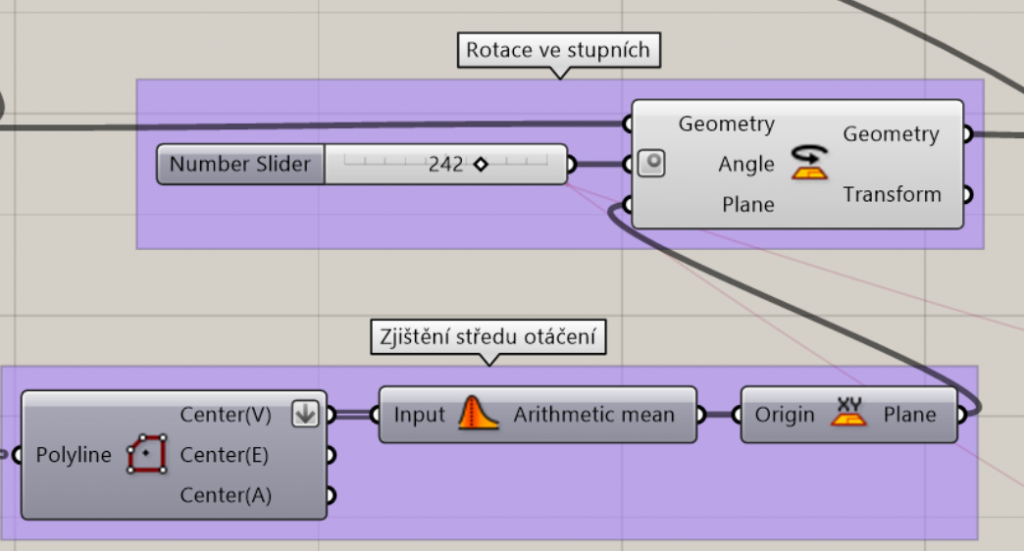
2f) Orientation to the cardinal points, or in this case facing the sun, is always very important factor when optimizing the insolation. I created the center of rotation of the volume using the Polygon center and Arithmetic mean functions, which together calculated the point located in the center of the project. Subsequently, it was enough to rotate the geometry along this point using the rotate component. The angle is given in degrees and can vary from 0 to 360.
____________________________________________________________________________________________________________
TEST #2
Using galapagos, I created a shape, where I connected the gene pool to the input, which generates the coordinates of the points of the ellipse, and in addition, I set the rotation angle of the shape as fitness to maximize the hours of sunshine.
Result:
Maximum achievable hours: 2600
Knowledge:
A very small ascetic form arises
All cells tend to fill any free spaces and move to have as many common sides as possible = forming a circle
Questions:
Is this the shape that fits the best configuration?
____________________________________________________________________________________________________________
Determination of criteria weights:
1) Area:
This criterion corresponded to the randomness of the shape, and generally the larger the area of the packaging, the more it was a design that fit my concept.
→ CRITERION OF EXTERIOR AESTHETICS that I want to maximize
2) Sunlight:
This criterion tended to be counterintuitive, but it did a much better job of optimizing the facade to receive the most possible light during periods when sunlight is scarce.
→QUALITY CRITERIA OF LIGHTING IN INTERIOR SPACES, which also needs to be maximized
3) Compromise:
In order to improve the design, I combine both criteria when it is not possible to maximize both, but when the goal is to create an optimal ratio of importance between them.
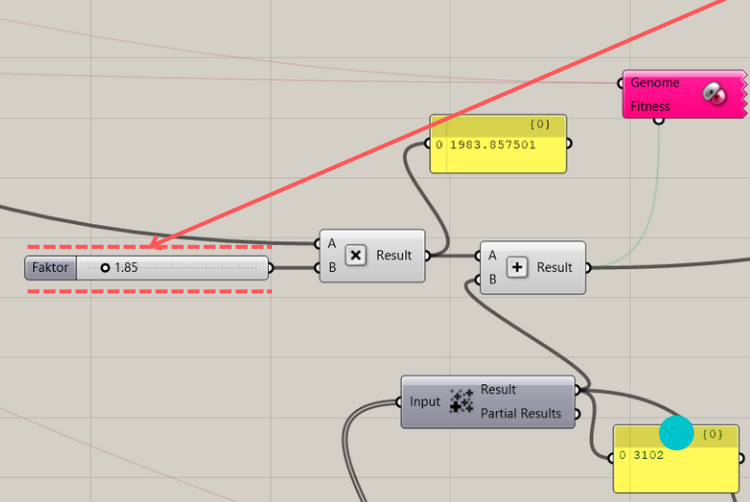
The aim was to give the criteria such weights that a meaningful result was created.
Several tests resulted in this calculation, which became the fitness for the galapagos component.
Allows the slider to change the importance of the area above the insolation. (the higher the number, the more the area is preferred)
____________________________________________________________________________________________________________
FINAL TEST
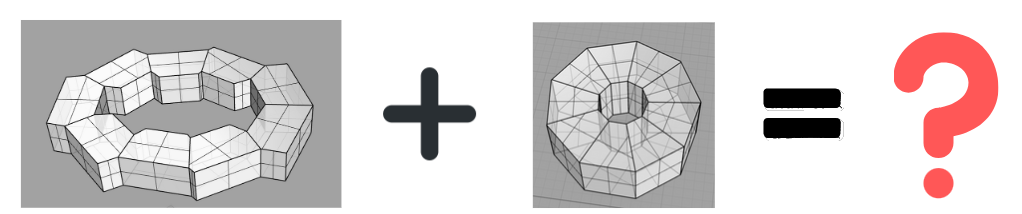
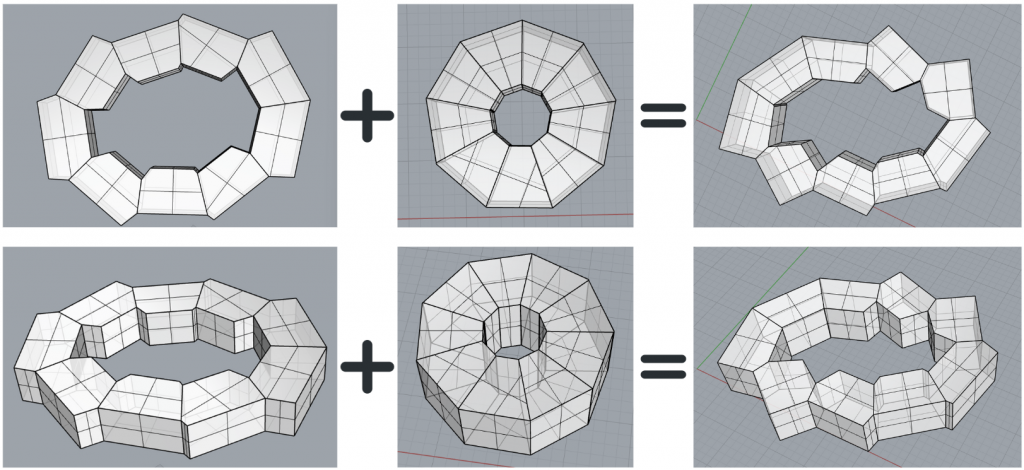
A shape is created that is a combination of criteria. It maximizes both surface and insolation with surface preference. (1.85x)

Area: 1589 m2 (that’s 97.7% of the maximum)
Sunshine: 1716 hours (that’s 66% of maximum)


CZECH PRESENTATION:
____________________________________________________________________________________________________________
Downloads:
____________________________________________________________________________________________________________
In this project i used LADYBUG TOOLS plug-in:
https://www.food4rhino.com/en/app/ladybug-tools
Thank you!

