The goal is to display various curves, spirals mostly, using polar coordinates.
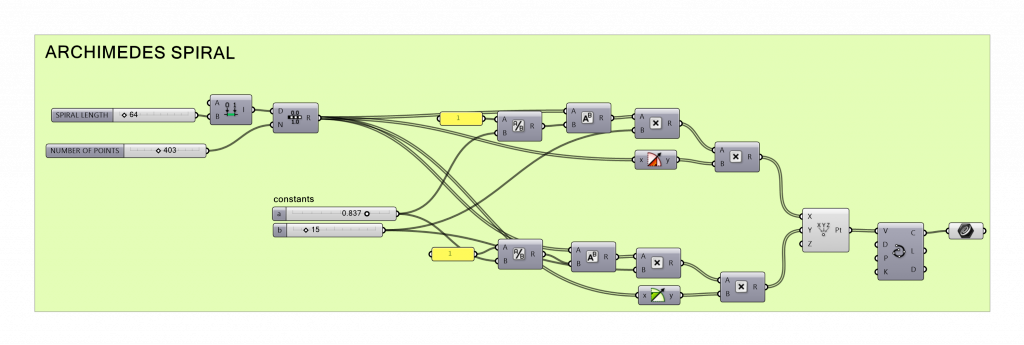
We start with Archimedes spiral.
Using Cartesian coordinates, we follow parametric equation expressed as:
k(t)=[a*t1/n*cost; a*t1/n*sint]
rewritten using GH compontents, our script looks like this:
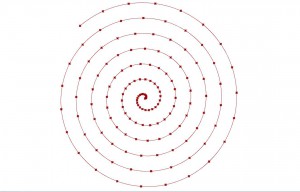
The result is a spiral, where we can control its size, length and collection of points forming the curve.
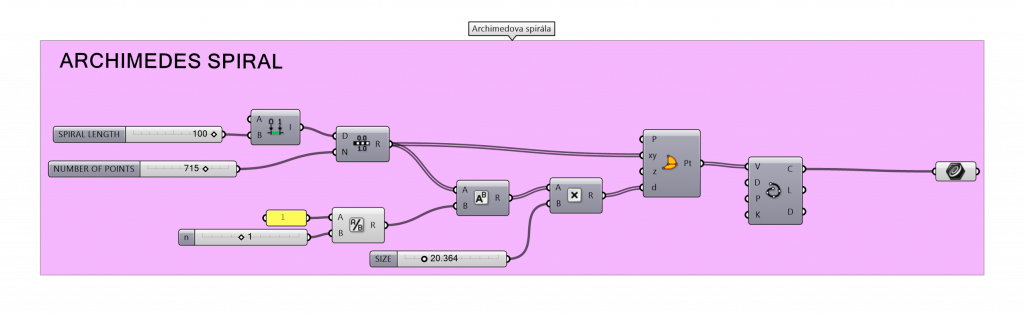
When using polar coordinates, we can achieve the very same result. However, the script is much easier. A polar equation is:
k(ϕ) = [a* ϕ1/n; ϕ]
When playing with parameter n, we can change a curvature of the spiral. In the following picture, n = -3, -2, -1, 1, 2, 4.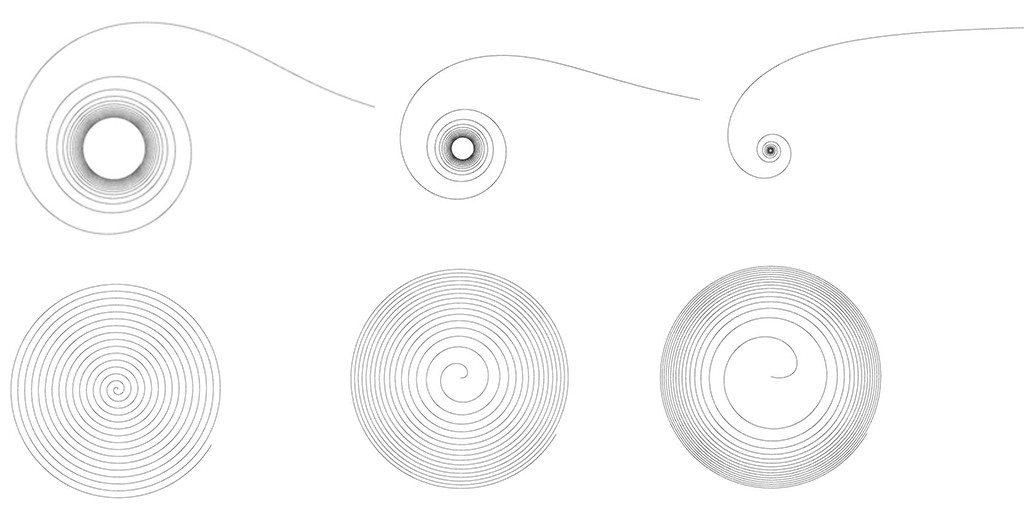
In the following examples, we use only polar coordinates, as we proved, they are more suitable for similar kinds of curves.
Next example is Hyperbolic spiral with polar equation:
k(ϕ) = [a/ ϕ; ϕ]
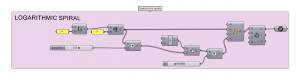
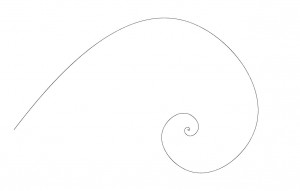
Logarhitmic spiral often occured in nature forms:
k(ϕ) = [a*e(b* ϕ) ; ϕ]
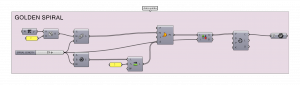
Golden spiral : (special type of logarithmic spiral)
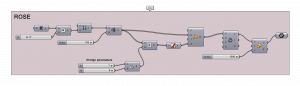
Another interesting geometrical form is so called “Rose“. We can change parameters to get different variations.
There are many spiral forms in 3D found in nature. I tried to imitate a snail shell using Archimedes spiral, but adding z-rotation. When getting a spiral in 3D, I divided the curve and constructed perpendicular circles of different radius. I made a surface either by loft. If you want the color to change, an option is to use ruled surface between circles.
Grasshopper file: