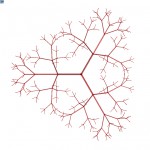
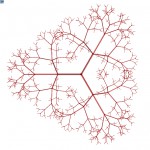
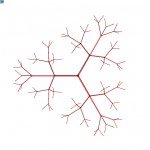
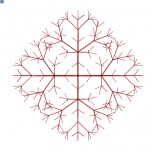
Project files: rekTree.3dm, rekTree.gh
Introduction
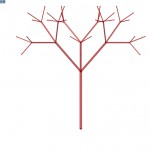
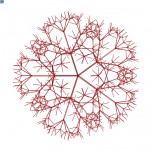
In this project, I combine the power of Grasshopper and C# programming language, to create models of trees generated from some basic parameters given as inputs. The product is somewhere between perfect fractal mathematical tree and actual natural result of biological processes.
Trees in nature are very complicated and their branches adapt to various influences such as their surrounding environment casting shadows, illnesses, animals, human-induced trimming, winds and varying seasons. For this project, I substituted those factors with mere randomness, since they, in effect, appear as randomness in the nature, too, and only a very observing person will see them as results of the influences.
This script allows for several parameters to be set, thus allowing to make very mathematical and precise trees with no space for randomness, but on the other hand enables the user to generate very unrealistic and overly random mixtures of branches, that could not exist in real world. The sweet spot in between is up to the artist’s eye to find.
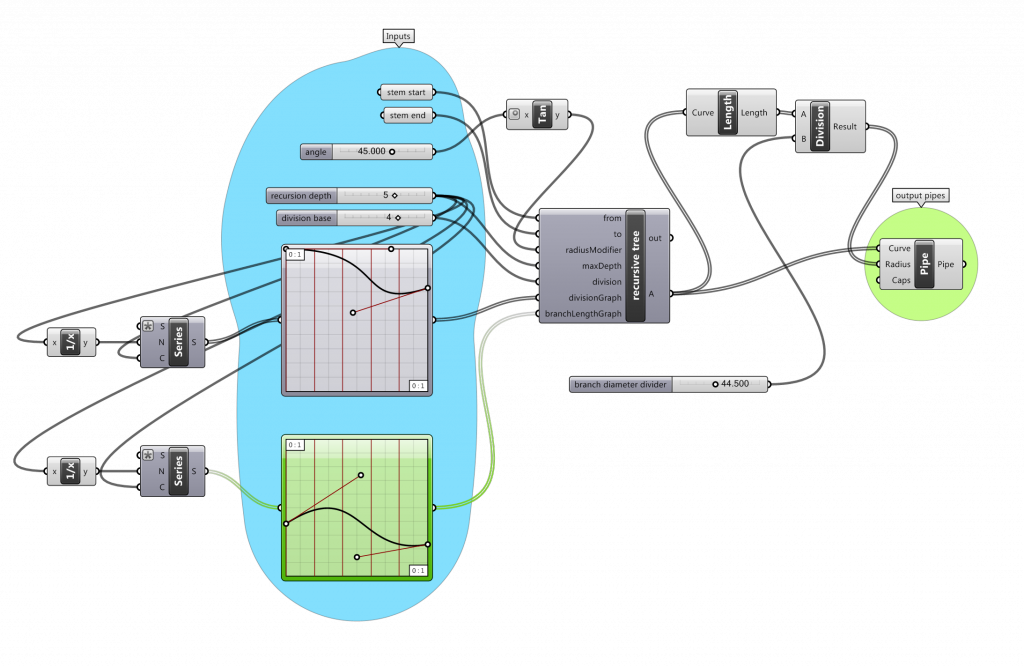
Grasshopper Scheme Explained
The blue bubble is marked as Inputs and that is what it is for.
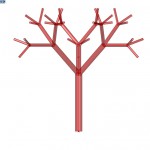
The two object inputs from Rhinoceros are just two points (stem start, stem end), which create the line of the first stem. It is recommended for those points to create line perpendicular to the ground (with the same X and Y coordinates).
For defining the angle at which the following branches rotate, there is the parameter angle, which in degrees defines rotation from normal (0 º would be continuing in a straight line, 90 º would be square rotation). This parameter is currently a little flawed and only works well until 45 º, probably due to the tangent function.

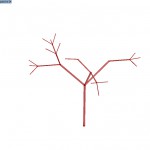
Angle of 15 º

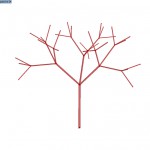
Angle of 30 º
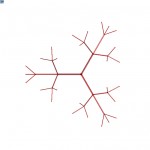
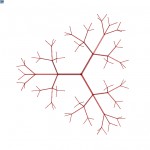
Another parameter, which is one of the more dangerous ones is recursion depth, and it defines how many branches does it take to stop dividing. This parameter can make the script run very slowly, since the amount of operation depends on this parameter exponentially.
The next parameter is division base and it defines how many maximum branches will be created at any division point. This greatly influences the look of the tree. It is also one of the dangerous parameters, since this amount is the base of potential exponential growth of required operations.
Following input is a graph and it defines the likelihood of the tree loosing a branch at certain level of depth. If it is a constant function of 1, it will not lose any. This parameter is very important and defines the character of the tree.
The other graph input defines the length of the branches depending on the level of depth. It is important to combine this graph with the previous one to create believable natural tree effect.
Both of the graphs show divisions by the current recursion depth (that’s what the 1/xs are for on the left)
On the right there are only a few functions transforming a List of Line Curves, the output of the C# script, via a pipe into a 3D tree instead of just set of lines. The parameter branch parameter divider defines the calculation of the pipes’ diameters.
And the most important part is of course the C# script, which is hidden within the recursive tree block in Grasshopper.
Script Explained
For this part, I understand that not everyone is familiar with programming, so I will attempt to explain every line of the code as for a layman. Every other line will start with double forward-slash (//) and be purple, which means it is the explanation of the previous line. The bolded words are names of variables, that can contain various data – numbers, points, lines, vectors etc.
private void RunScript(Point3d from, Point3d to, double radiusModifier, int maxDepth, int division, List divisionGraph, List branchLengthGraph, ref object A){ // is mandatory definition of the function, setting what variables it will get from the Grasshopper Block; those parameters are the same ones discussed previsously; the ref object A is the output double moverModifier = 1; // real variable, works similarly to the branch length parameter, but is now firmly set to 1 ~ no change Vector3d branch = new Vector3d((to.X - from.X), (to.Y - from.Y),(to.Z - from.Z)); // creates a vector from the provided two points (from and to) List output = new List(); // creates a list of general objects to be used as output at the end LineCurve rodic = new LineCurve(from, to); // creates a LineCurve type object from the provided two points rekVet(0, maxDepth, rodic, radiusModifier, moverModifier, ref output, from, division, divisionGraph, branchLengthGraph); // runs a first level of depth (notice the 0) of the recursive (run within itself) function, prividing needed parameters and the LineCurve, which it will be based off of; the output variable is given as ref, so the function can change it's content and it will be saved within the whole program. A = output; // saves the contents of output to variable A, thus making it accessible for the Grasshopper outside } // closes the function private void rekVet(int depth, int maxDepth, LineCurve rodic, double radiusModifier, double moverModifier, ref List output, Point3d from2, int division, List divisionGraph, List branchLengthGraph){ // this is the recursive function, which takes the needed parameters, creates required branches and then runs again for each of the branches, creating the divisions if(depth < maxDepth){ // checks if we are within the maximal depth - without this check the program would go deeper and deeper and never stop Random rand = new Random(Guid.NewGuid().GetHashCode()); // generates an object of type Random, based on some everchanging computer stuff, which works as random number generator double randomer = rand.NextDouble(); // creates a random number between 0 and 1 if(randomer <= divisionGraph[depth]){ // based on the first graph parameter decides, whether to continue dividing or not double branchLengthModifier = branchLengthGraph[depth] * moverModifier; // based on the second graph parameter decides what length multiplier will be used Vector3d branch = new Vector3d(rodic.PointAtStart.X - rodic.PointAtEnd.X, rodic.PointAtStart.Y - rodic.PointAtEnd.Y, rodic.PointAtStart.Z - rodic.PointAtEnd.Z); // creates a vector from the previous branch (parent branch) double radius = radiusModifier * branch.Length; // variable radius helps create the new brances of the right size Point3d to = new Point3d(rodic.PointAtEnd.X, rodic.PointAtEnd.Y, rodic.PointAtEnd.Z); // new point identical to the parent branch starting point Point3d from = new Point3d(rodic.PointAtStart.X, rodic.PointAtStart.Y, rodic.PointAtStart.Z); // new point identical to the parent branch ending point Plane aimPlane = new Plane(to, branch); // new plane perpendicular to parent branch and going through the ending point Circle cil = new Circle(aimPlane, radius * branchLengthModifier); // makes circle on the previous plane with the defined radius Point3d spodni = cil.ClosestPoint(from2); // creates a point on the circle which is closest to the bottom of the whole tree output.Add(rodic); // adds the parent branch to the list of output lines LineCurve vetev1 = new LineCurve(to, new Point3d(spodni.X - branch.X * branchLengthModifier, spodni.Y - branch.Y * branchLengthModifier, spodni.Z - branch.Z * branchLengthModifier)); // creates new branch going from the endpoint of parent branch to the new point (the closest to the bottom one) double newDivision = division * divisionGraph[depth]; // variable containing the amount of new divisions based on the graph parameter for(int i = 0; i < newDivision; i++){ // starts cycle running repeatedly based on how many divisions we now need LineCurve vetev2 = new LineCurve(vetev1); // creates new branch identical to the previous branch vetev2.Rotate((i * 2 * 3.14159265 / Math.Round(newDivision)), branch, to); // rotates this branch around the parent branch by an angle of 360° divided by the amount of divisions rekVet(depth+1, maxDepth, vetev2, radiusModifier, moverModifier, ref output, from2, division, divisionGraph, branchLengthGraph); // runs the function we are inside again with a little different paremeters (the depth increased and branch is now the new branch, not the parent); this is the important part for the function to work recursively } // closes the cycle and runs it again if needed (based on the divisions) } // closes the test if we should divide or not } // closes the test if we aren't too deep } // closes the recursive function
So essentially, the script gets a branch and processes it with a subprogram. The subprogarm decides how many new branches will grow out of it, at what angle, what length they will be and if they will even grow at all. It creates those branches and processes all of them again in the same subprogram, going deeper to the hierarchy of the tree. When the subprogram is deep enough, it stops making more branches.
Potential Improvements of the Script
- The C# script itself is very messy and not efficient. For example the way I pass the constant variables to the following iterations of the recursive function (probably, if I understand it correctly) saves the variables again for each iteration. This could all be replaced by a single struct type object, that would contain them and be passed as reference.
- Other than that the method I used for creating the new branch is weird, but I couldn’t find anything better provided the objects that are offered by Rhino. Ther are probably some unused parts in the script. I even deleted some for this presentation, which stayed in the .gh file.
- I also multiple times convert points to LineCurve and then get those points back from it. This is due to the fact that only the LineCurve object had the methods for rotation I needed and is also sort of different from normal line, so I got the points in this weird way to be sure. This makes weird duplicity in the vectors and points I have there, that could be passed through the function without those redundant operations (probably).
- Currently the randomness of the trees is based on an internal state of a computer, thus disabling the option to save a ‘seed’ of the tree and generate identical in the future. This is possible to fix with some more understanding of C#.
Bottomline and Future
- I believe it is possible to generate a quite believable trees with this method, but not any type. This script could be a proof of concept for future development of the tree script. Although there is a big competition on the market, I can imagine improvements for some other bigger projects (such as CGI landscape generation).
- My main ideas for improvement would be ability of the branches to be aware of their surroundings and react to it, thus preventing such things as two branches growing too close of even intersecting. The overall reactiveness to the environment of the whole tree would be pretty, too.
- Another thing would be support for more differentiated types of trees. There are many typologies of trees and this script covers just small part of them. This would require fundamental remaking of the whole program, so this would be just practice for it.
- To add realism, there should be way to manage each branch and make it a little curvier/bendy. Together with smart placement of bark, this could add a lot to realism.
- A big thing would be adding leaves. This topic could be for another recursive function on it’s own. Basically ending the ‘wood’ part of the tree and continuing with the ‘softer’ stems of leaves up to their little veins.
- Adding roots would be similar job as the tree, but instead in the other way. They have different topology, but in essence are a tree underground.
- Studying and working with dendrologists would probably help understanding the way trees grow to detail and allow for much more complicated nature-simulating script to be made.
I wasn’t used to C# so much, so there are inefficiencies. I think the tree project in general has some potential, now it is important to decide if it is worth it to delve into a topic, that seems to be quite popular and has a lot of competition.
This Project was done within the course CAD IV – Scripting, taught by Šimon Prokop at the Faculty of Architecture of Czech Technical University in Prague.
Done in summer term of academic year 2014/2015 by Martin Vancl, student of second year at FA CTU and first year at FIT CTU.
Contact: Martin Vancl for information on the project or Šimon Prokop for more information on the course